Un sistema de una ecuación lineal comprende dos o más ecuaciones y se busca una solución común a las ecuaciones. En un sistema de ecuaciones lineales, cada ecuación se corresponde con una recta y se busca el punto de intersección de las dos rectas.
Ejemplo:
Resuelve el siguiente sistema de ecuaciones lineales:
y=2x+4
y=3x+2
Como estamos buscando el punto de intersección, podemos graficar las ecuaciones:
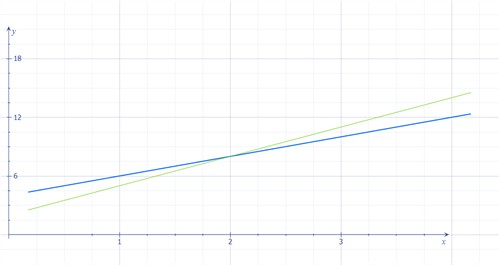
Aquí vemos que las rectas se intersecan en el punto x = 2, y = 8. Esta es nuestra solución y podemos referirnos a ella como solución gráfica de la tarea.
Pero, ¿cómo se llega a una solución si las rectas nunca se cruzan? No se puede, el sistema de ecuaciones no tiene solución.
También se puede llegar a la respuesta correcta con la ayuda del método de eliminación (también llamado método de adición o de combinación lineal) o del método de sustitución.
Cuando se utiliza el método de sustitución se aprovecha el hecho de que si dos expresiones y y x son de igual valor x=y, entonces x puede sustituir a y o viceversa en otra expresión sin cambiar el valor de la expresión.
Ejemplo:
Resuelve los sistemas de ecuaciones utilizando el método de sustitución
y=2x+4
y=3x+2
Sustituimos la y de la ecuación superior por la expresión de la segunda ecuación:
2x+4=3x+2
4−2=3x-2x
2=x
Para determinar el valor de y, podemos proceder insertando nuestro valor de x en cualquiera de las ecuaciones. Seleccionamos la primera ecuación:
y=2x+4
Introducimos x=2 y obtenemos
y=2⋅2+4=8
Así hemos llegado precisamente a la misma respuesta que en la solución gráfica.
El método de eliminación requiere que sumemos o restemos las ecuaciones para eliminar x o y, a menudo no se puede proceder a la suma directamente sin multiplicar primero la primera o la segunda ecuación por algún valor.
Ejemplo:
2x-2y=8
x+y=1
Ahora queremos sumar las dos ecuaciones pero no se eliminará ni la x ni la y. Por lo tanto, debemos multiplicar la segunda ecuación por 2 en ambos lados y obtener
2x-2y=8
2x+2y=2
Ahora intentamos sumar nuestro sistema de ecuaciones. Comenzamos con los términos x a la izquierda, y los términos y a continuación y finalmente con los números del lado derecho:
(2x+2x)+(-2y+2y)=8+2
Ahora se han eliminado los términos y y tenemos una ecuación con una sola variable:
4x=10
x=10/4=2.5
A continuación, para determinar el valor de y introducimos x=2,5 en una de las ecuaciones. Seleccionamos la primera:
2⋅2.5−2y=8
5−8=2y
−3=2y
-3:2=y
y=-1.5



