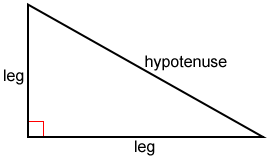
El lado opuesto al ángulo recto de un triángulo rectángulo se llama hipotenusa. Los lados que forman el ángulo recto se llaman catetos o, a veces, el lado adyacente u opuesto (relativo a uno de los ángulos del triángulo que no es el ángulo recto), según el contexto.
La longitud de un lado de un triángulo corresponde al tamaño del ángulo opuesto al lado. Dado que la hipotenusa de un triángulo rectángulo es el lado más largo del triángulo, el ángulo de 90 ° opuesto también es el ángulo más grande del triángulo rectángulo. Esto también tiene sentido porque los ángulos internos de un triángulo suman 180 °. Dado que todos los triángulos tienen 3 lados y 3 ángulos internos, es imposible que un triángulo rectángulo tenga otro ángulo mayor o igual a 90 °, porque el tercer ángulo tendría que ser 0 ° o tener una medida de ángulo negativa.
Cómo encontrar la hipotenusa de un triángulo rectángulo
La hipotenusa de un triángulo rectángulo se puede encontrar usando el Teorema de Pitágoras , que es un teorema específico de los triángulos rectángulos. No se puede usar con triángulos que no sean rectángulos. Para un triángulo rectángulo con una hipotenusa de longitud cy longitudes de cateto a y b:
o
Ejemplo:
Encuentre la longitud de la hipotenusa del triángulo a continuación.

Dadas las piernas a=15 yb=20:
c 2 =15 2 + 20 2
c 2 =625
c=25
Entonces, la longitud de la hipotenusa es 25.
También es posible encontrar la hipotenusa de un triángulo dado un lado y un ángulo del triángulo, sin embargo, esto requiere el uso de trigonometría. Consulte la sección trigonometría para obtener más detalles. Brevemente, dado el siguiente triángulo rectángulo
las siguientes relaciones se pueden usar para encontrar los distintos lados y ángulos de un triángulo rectángulo:
sin (A)=; sin (B)=
cos (A)=; cos (B)=
tan (A)=; tan (B)=
En las relaciones anteriores, A, B y C son los ángulos del triángulo opuestos a los lados a, byc, respectivamente.



