Todas las criaturas de la Tierra comparten un cierto vínculo común. No es un elemento complicado, profundamente oculto o una conexión de otro mundo; es solo una simple verdad. Todos entramos en la existencia en algún momento, y todos dejamos nuestras existencias en otro punto de la línea.
Entre esos puntos de inicio y final, cada uno de nosotros tiene sus propias experiencias. Algunas se comparten con otras personas mientras que otras son puramente internas, pero todas nos afectan de una forma u otra. ¿Son todos estos eventos puramente aleatorios, o hay alguna rima y razón detrás de ellos?
Muchos filósofos, maestros, matemáticos e hígados de vida en general creen que nada es aleatorio. Un hombre nacido en Italia hace más de 800 años entra en esta categoría. Su nombre era Leonardo Pisano Bogollo, pero hoy lo conocemos como Fibonacci. Desarrolló un amor por los números a una edad temprana, y esta pasión lo llevó a un descubrimiento capaz de cambiar la forma en que las personas ven la vida y el mundo que los rodea.
La secuencia de Fibonacci cobra vida
Algunos creen que si miras lo suficientemente de cerca, puedes encontrar un patrón en cualquier cosa. Esto puede muy bien ser cierto, pero Fibonacci pudo extraer un patrón específico de su conocimiento de los números y demostrar que, posiblemente, podría continuar para siempre. Señaló la secuencia de Fibonacci en su primer libro, Liber abacci, donde planteó un problema verbal de base matemática para que todos reflexionaran.
“Un hombre puso un par de conejos en un lugar rodeado por una pared. ¿Cuántas parejas de conejos se pueden producir a partir de esa pareja en un año si se supone que cada mes cada pareja engendra una nueva pareja a partir de la cual el segundo mes en adelante se vuelve productivo?
¡Este puede ser un buen momento para hacer una taza de café y averiguar el paradero de la aspirina porque su mente está a punto de volar!
¡Bien, aquí vamos! Verás, Fibonacci razonó que los conejos alcanzarían la madurez y se aparearían en aproximadamente un mes, por lo que después de un mes, todavía había solo un par de conejos. Dado que su período de gestación también es de un mes, el segundo mes llegó a su fin con solo un par. Sin embargo, al final de ese tercer mes, apareció un segundo par. Las hembras deberían poder parir una vez al mes después de su primera camada, por lo que el cuarto mes vio a la primera pareja producir otra.
El quinto mes llegó y el par uno se reprodujo de nuevo, mientras que el par dos hizo lo mismo. En este punto, el gran total era de cinco pares. En pocas palabras, al final del año, 377 parejas vivían dentro de los límites del muro.
Mirando un poco más profundo
Por supuesto, Fibonacci dio algunos saltos bastante audaces antes de pronosticar la fecundidad de esta pelusa. Su escenario giraba en torno a unas condiciones muy controladas. Por ejemplo,
- Cada nueva camada constaba de dos conejos: un macho y una hembra
- Todos eran físicamente capaces de reproducirse
- Cada hembra pudo comenzar el proceso reproductivo al mes de edad y dar a luz a una nueva camada cada mes a partir de entonces.
- Todos pasaron todo el año sin sucumbir a una enfermedad o ser expulsados del recinto por los otros conejos.
De hecho, algunos conejos pueden tardar cuatro meses o más en alcanzar la madurez. Pueden nacer hasta 12 crías en una sola camada, y no se garantiza que todas sobrevivan. Sin embargo, cuando lo piensas realmente, los números incontrolados y la selección natural ciertamente podrían compensarse entre sí. Las bien pensadas condiciones de Fibonacci podrían fácilmente dar cuenta de todas las posibilidades y equilibrar la balanza.
Todas estas ideas pueden parecer un poco abstractas en forma escrita. Por supuesto, las matemáticas de Fibonacci son acertadas. Una vez que pones los números donde están las palabras, se vuelve un poco más claro. En la secuencia de Fibonacci, comienzas con 0 y 1, y continúas desde allí. En pocas palabras, dice así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 y así sucesivamente.
Cada nuevo número de la secuencia se crea sumando los dos números anteriores.
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
Puede continuar indefinidamente, sumando los dos últimos números de la secuencia para revelar el siguiente. Si bien la explicación suena prolongada y compleja, en realidad es bastante simple. Sin embargo, las cosas se complican un poco más a partir de este punto.
El concepto toma forma
Estamos a punto de llevar esto a un nivel completamente nuevo aquí. Imagina los números de la secuencia de Fibonacci representados por cuadrados como los de una hoja de papel cuadriculado. Busque un punto de partida en algún lugar cerca del centro de la página y coloree un solo cuadrado que represente el primer número de la secuencia (1). Junto a él, haz lo mismo en honor al segundo. Luego, siendo dos el tercer número, use un color diferente para sombrear un espacio cuadrado de 2 por 2. A partir de ahí, busque un tono diferente para colorear en un espacio de 3 por 3 cuadrados y así sucesivamente. Terminará con una versión vibrante de este ejemplo:
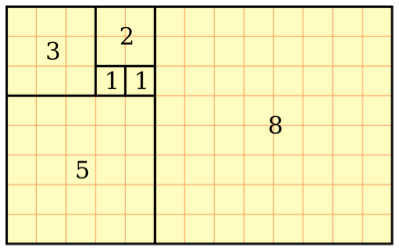
¿Notas cómo encajan perfectamente como piezas de un rompecabezas? El siguiente número de la serie sería 13, y la figura que toma forma aquí mide 13 cuadrados de ancho. A medida que avanza por los números más grandes, el patrón sigue siendo el mismo. Cada nuevo cuadrado será más grande que el siguiente, pero siguiendo los números de la secuencia de Fibonacci, siempre encajarán perfectamente en su lugar en proporción exacta a los anteriores.
Ahora, si lo está siguiendo en papel, tome un bolígrafo. Comience en la esquina superior de su primer cuadrado y dibuje la primera etapa de una espiral que corra hacia su esquina opuesta, cortando el cuadrado por la mitad. Continúe su línea a través del siguiente bloque individual y a través de los siguientes, dibujando su espiral a través del centro diagonal de cada cuadrado más grande. Terminarás con algo como esto:

La espiral de Fibonacci y el rectángulo creado por su secuencia de números se conocen como el Rectángulo Áureo debido a su conexión con la Proporción Áurea. Como número, esta figura mágica es 1.61803 y está representada por la letra griega Phi (Φ). Puede parecer que estamos saltando un poco, pero todo esto es realmente relevante.
En geometría, la proporción áurea se crea cuando divide una línea en dos partes, pero no solo en dos partes. La línea debe dividirse en el lugar correcto donde toda la línea dividida por la longitud de la porción más larga de su división sea exactamente igual al segmento más largo dividido por el más corto. Lo has adivinado: ambas cifras deben ser iguales a 1,61803.
Se dice que los rectángulos creados con la proporción áurea son los más agradables que jamás haya visto. Esto nos devuelve a Fibonacci. Resulta que cuando tomas dos números sucesivos cualesquiera en su secuencia y encuentras su proporción dividiendo el más grande por el más pequeño, está extremadamente cerca del antiguo estándar dorado. ¡Ver este!
21/13 = 1,61538
89/55 = 1,47272
121393/75025 = 1,61803
¡Mira eso! ¡Encontramos un ganador! Habiendo dicho todo eso, la Secuencia de Fibonacci, el Rectángulo Dorado y su espiral inherente están a nuestro alrededor. Estás a punto de descubrir cómo y dónde.
Espiral hacia el control total
Antes de seguir leyendo, debe estar absolutamente seguro de que está listo para dar este salto. Este es solo un pequeño consejo amistoso. Una vez que lo ve, no puede dejar de verlo, ¡y le cambiará la vida!
El Rectángulo Dorado generado por la Secuencia de Fibonacci ha estado apareciendo en todo el mundo durante siglos. Un ejemplar principal es el Partenón de Grecia. Numerosos ejemplos de la Proporción Áurea y el Rectángulo se encuentran por dentro y por fuera, tanto a gran como a pequeña escala.
La Mona Lisa de Leonardo da Vinci podría considerarse otra muestra de la proporción casi áurea en acción. Se dice que sus dimensiones son de 30 pulgadas por 21 pulgadas. Al seguir el plan estándar, el lado más grande del rectángulo dividido por el más pequeño llega a 1.42857. No es una coincidencia exacta, pero está cerca.
Rumbo a Egipto, encontramos otro posible ejemplo en la Gran Pirámide de Giza. La más grande de las tres pirámides, esta mide 756 pies de ancho y 481 pies de alto. Cuando haces los cálculos, la razón es 1.57172; de nuevo, está justo en el límite.
El artista Piet Mondrian también inserta la secuencia de Fibonacci en algunas de sus pinturas. Puede ver claramente los cuadrados de las piezas del rompecabezas que componen el Rectángulo Dorado en ciertos ejemplos de su trabajo. Si lo mira el tiempo suficiente, el ojo de su mente puede incluso comenzar a dibujar en espiral.
Estos son solo algunos casos ampliamente conocidos de este patrón que se ha trabajado en el arte, la arquitectura y la ingeniería a lo largo de los siglos. Mucha gente insiste en que es mera coincidencia, refiriéndose al hecho de que puedes encontrar patrones en casi cualquier cosa si los estás buscando. En esa misma línea, algunos de estos casos surgieron mucho antes que el propio Fibonacci.
Muchos lo atribuyen todo a lo obvio. Algunas de las mentes más brillantes y estéticas de la historia están detrás de la realización de esas producciones. La lógica pura dicta que incorporarían las dimensiones más agradables visualmente en su trabajo, incluso si es en un nivel subconsciente.
Puede racionalizar la situación de muchas formas diferentes, pero es aún más profunda. Ciertas cosas no pueden ignorarse ni explicarse.
Solo es natural
Si sales y miras a tu alrededor, también encontrarás Fibonacci en la naturaleza, y no solo en uno o dos lugares diferentes. Los girasoles son un buen ejemplo. Esos pétalos de color amarillo brillante rodean una gran masa de semillas, pero las semillas no están dispuestas al azar; se enrollan con gracia desde el centro de la cabeza de la semilla.
Las piñas son otro ejemplo muy utilizado. Notarás que sus picos están dispuestos en espirales desde las perspectivas en sentido horario y antihorario. Lo mismo ocurre con las piñas. Si tienes un arbusto de acebo cerca o algún tipo de arbusto similar, échale un vistazo. Al principio, las hojas parecen crecer al azar o incluso en patrones circulares. Tras un examen más detenido, verá que en realidad están un poco escalonados, corriendo en ásperas espirales desde la punta hasta el tronco.
La humanidad también exhibe pequeños fragmentos del Rectángulo Dorado. Los rostros humanos adultos promedio miden de ocho a nueve pulgadas de largo por seis a siete pulgadas de ancho. Si calcula la proporción de los dos extremos, llega a 1,5, que está dentro de una fracción de la proporción áurea. El cabello humano tiende a crecer hacia afuera en espirales desde un punto central. De aquí en adelante, comenzará a ver la versión de la secuencia dondequiera que mire. ¡No digas que no te lo advertimos de antemano!
Haciendo las matemáticas
Como es el caso con la mayoría de situaciones matemáticas, existen reglas para calcular números en esta serie. Viene completo con su propia variedad de fórmulas. En primer lugar, veamos una demostración de la regla general que rodea a la secuencia de Fibonacci:
xn = xn-1 + xn-2
Aquí, «n» le da a cada número de la Serie Fibonacci un número correspondiente en nuestra secuencia tradicional: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 …
«Xn» representa los números en la secuencia de Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
Usando la regla, podemos calcular un número en la secuencia. Probemos el séptimo:
x7 = x7-1 + x7-2
x7 = x6 + x5
x7 = 8 + 5
x7 = 13
En realidad, es solo otra forma de decir: «Un número específico en la secuencia de Fibonacci es igual a la suma de los dos números anteriores».
A partir de aquí, solo se vuelve más complejo e involucrado. Encontrarás cualquier cantidad de ecuaciones y explicaciones relacionadas con la inducción matemática, la recurrencia lineal, el trazado de la secuencia en gráficos, etc.
Estas fórmulas son griegas, perdona el juego de palabras, para aquellos que intentan saltar de cabeza al extremo avanzado del espectro. A menos que tenga algunos antecedentes sobre las técnicas reales de resolución de problemas que se utilizan aquí, es mejor familiarizarse con la situación. Una vez que comprenda los conceptos básicos como la fórmula anterior, es una simple cuestión de dar pequeños pasos a partir de entonces.
General
Todos tenemos vínculos comunes. Si son aleatorios y coincidentes o productos de secuencias matemáticas subyacentes y un caos misteriosamente ordenado es en gran parte una cuestión de opinión. Independientemente de su posición sobre el tema, ciertos patrones no pueden pasarse por alto ni descartarse fácilmente. Fibonacci vio esto incluso cuando era niño, y el trabajo de su vida desencadenó una secuencia imparable de eventos.



