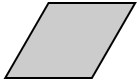
El área de un rhombus es el espacio contenido dentro de su perímetro . Un rombo es un paralelogramo en el que todos los lados son congruentes. El espacio gris es el área del rombo en el siguiente diagrama.
Fórmula de área
Hay varias fórmulas que se pueden usar para encontrar el área de un rombo dependiendo de los parámetros conocidos.
Uso de diagonales
El área, A, de un rombo es la mitad del producto de sus dos diagonales.
donde d 1 y d 2 son las longitudes de las dos diagonales.

Haciendo referencia al rombo ABCD anterior, sea AC=d 1 y BD=d 2 . Las diagonales de un rombo son perpendiculares entre sí, por lo que AC⟂ DB. Rhombus ABCD se puede descomponer en triángulos ABC y ADC.
El área de △ ABC=donde BE es la altitud de △ ABC. El área de △ ADC=
donde DE es la altitud de △ ADC. El área del rombo ABCD es igual a la suma de las áreas de △ ABC y △ ADC.
| △ ABC + △ ADC= | |
| = | |
| = | |
| = |
Ejemplo:
Si el área de un rombo es 230 y una de sus diagonales es 10, ¿cuál es la longitud de la otra diagonal?
Sea d 1 =10. Dado que A=230 podemos encontrar d 2 de la siguiente manera:
230=5 × d 2
d 2 =46
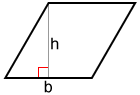
Uso de lado y altura
Dado que un rombo también es un paralelogramo, podemos usar la fórmula para el área de un paralelogramo:
A=b × h
donde b es la base o la longitud del lado del rombo y h es la altura correspondiente.
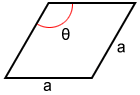
Uso de lados y ángulos
Si se dan la longitud del lado y uno de los ángulos del rombo, el área es:
A=a 2 × sin (θ)
donde a es la longitud del lado y θ es uno de los ángulos.
Encontrar área usando una cuadrícula
Otra forma de encontrar el área de un rombo es determinar cuántos cuadrados unitarios se necesitan para cubrir su superficie. A continuación se muestra un cuadrado unitario cuyas dimensiones son de 1 cm.
Se puede usar una cuadrícula de cuadrados unitarios para determinar el área de un rombo.
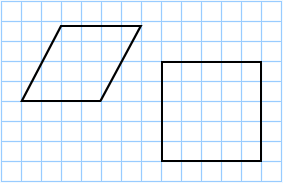
La cuadrícula de arriba contiene cuadrados unitarios que tienen un área de 1 cm 2 cada uno. El rombo de la izquierda contiene 8 cuadrados completos y 12 cuadrados parciales, por lo que tiene un área de aproximadamente:
El rombo de la derecha contiene 25 cuadrados completos, por lo que tiene un área de aproximadamente 25 cm 2 .
Este método se puede utilizar para encontrar el área de cualquier forma; no se limita a rombos. Sin embargo, es solo un valor aproximado del área. Cuanto más pequeña sea la unidad cuadrada utilizada, mayor será la precisión de la aproximación. Usar una cuadrícula formada por cuadrados de 1 mm es 10 veces más preciso que usar una cuadrícula formada por cuadrados de 1 cm.



