El perímetro es la longitud o distancia total alrededor de una forma bidimensional. En la siguiente figura, el perímetro de cada forma es la suma de las longitudes de cada lado, que se muestran en rojo. El perímetro de un círculo o elipse se denomina circunferencia . . Para un polígono , el perímetro es la suma de las longitudes de sus lados.
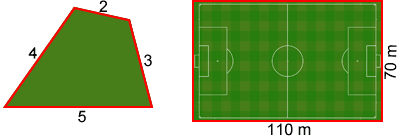
El perímetro del cuadrilátero de arriba es 2 + 3 + 4 + 5=14. El perímetro del campo de fútbol de arriba es 110 + 110 + 70 + 70=360 metros. Para agregar una valla alrededor de los bordes de todo el campo de fútbol, la valla tendría que cubrir 360 metros.
Perímetro de figuras geométricas comunes
A continuación se muestran fórmulas para los perímetros de algunas figuras geométricas comunes.
Cuadrado
El perímetro de un cuadrado con una longitud de lado s es:
P=4s

Rectángulo
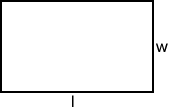
El perímetro de un rectángulo con largo, l, y ancho, w, es.
P=2l + 2w
Triángulo equilátero
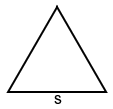
El perímetro de un triángulo equilátero con lados de longitud s es:
P=3s
Polígono regular
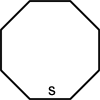
El perímetro de un polígono de n lados regular (todos los lados son iguales) con longitudes de lado s es:
P=ns
Círculo
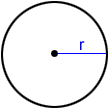
La circunferencia de un círculo con radio r es:
C=2πr
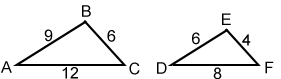
Perímetro de figuras similares
Si las figuras geométricas son similares, la razón de sus perímetros es igual a las razones de sus lados correspondientes. Para los triángulos similares ABC y DEF a continuación,