El Origen de la Geometría surgió a partir de los estudios de los primeros matemáticos para comprender las medidas de un objeto o campo.
Pitágoras demostró que las diversas leyes de la geometría primitiva, se pueden deducir estableciendo un número de axiomas y postulados. Así surgió el conocido Teorema de Pitágoras que afirma que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Surgió la geometría demostrativa que estudiaba y analizaba polígonos y círculos y de sus figuras tridimensionales. Esta Geometría fue estudiada por Euclides con muchas más profundidad en sus Libros, que hoy conocemos como: Los Elementos de Euclides.
Esta es una traducción del artículo de Michel Serres.
Renan tenía las mejores razones del mundo para llamar milagroso el advenimiento de las matemáticas en Grecia. La construcción de idealidades geométricas o el establecimiento de las primeras pruebas fueron, después de todo, eventos muy improbables. Si pudiéramos formarnos una idea de lo que sucedió alrededor de Tales y Pitágoras, avanzaríamos un poco en filosofía. Los comienzos de la ciencia moderna en el Renacimiento son mucho menos difíciles de entender; esto fue, a fin de cuentas, solo una repetición. Dando testimonio de este milagro griego, tenemos a nuestra disposición dos grupos de textos. Primero, el corpus matemático mismo, tal como existe en los Elementos de Euclides, o en otros lugares, tratados formados por fragmentos. Por otro lado, la doxografía, las historias dispersas a la manera de Diógenes Laercio, Plutarco o Ateneo, varios comentarios de Aristóteles, o las notas de comentaristas como Proclus o Simplicius. Es un eufemismo decir que estamos tratando aquí con dos grupos de textos; De hecho, estamos tratando con dos idiomas. Ahora, hacer la pregunta del comienzo griego de la geometría es precisamente preguntar cómo se pasa de un idioma a otro, de un tipo de escritura a otro, del idioma que se dice que es natural y su notación alfabética al lenguaje riguroso y sistemático. de números, medidas, axiomas y argumentos formales. Lo que nos queda de toda esta historia no presenta más que dos idiomas como tales, narraciones o leyendas y pruebas o figuras, palabras y fórmulas. Por lo tanto, es como si nos enfrentáramos con dos líneas paralelas que, como es bien sabido, nunca se encuentran. El origen retrocede constantemente, inaccesible, irrecuperable. El problema está abierto.
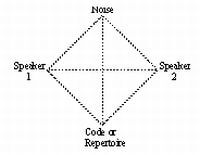
He tratado de resolver esta pregunta tres veces. Primero, sumergiéndolo en la tecnología de las comunicaciones. Cuando dos hablantes tienen un diálogo o una disputa, el canal que los conecta debe dibujarse mediante un diagrama con cuatro polos, un cuadrado completo equipado con sus dos diagonales. Por ruidosa o irreconciliable que sea su disputa, por calmada o tranquila que sea su acuerdo, están vinculados, de hecho, dos veces: necesitan, antes que nada, una cierta intersección de sus repertorios, sin la cual seguirían siendo extraños; Luego se unen contra el ruido que bloquea el canal de comunicación. Estas dos condiciones son necesarias para el diálogo, aunque no suficientes. En consecuencia, los dos oradores tienen un interés común en excluir a un tercer hombre e incluir a un cuarto, ambos prosopopeias de los poderes del ruido o de la instancia de intersección. (1) Ahora este esquema funciona exactamente de esta manera en Platón Los diálogos, como se puede mostrar fácilmente, a través del juego de personas y sus nombres, sus semejanzas y diferencias, sus preocupaciones miméticas y la dinámica de su violencia. Ahora bien, y sobre todo, los sitios matemáticos, desde el Meno hasta el Timeo, pasando por el estadista y otros, se pueden reducir geométricamente a este diagrama. Cuando aparece el origen, pasamos de un idioma a otro, el lenguaje que se dice que es natural presupone un esquema dialéctico, y este esquema, dibujado o escrito en la arena, como tal, es la primera de las idealidades geométricas. La matemática se presenta como un diálogo exitoso o una comunicación que domina rigurosamente su repertorio y es purgado al máximo del ruido. Por supuesto, no es tan simple. Lo irracional y lo indescriptible residen en los detalles; escuchar siempre requiere cotejar; siempre queda un residuo o un residuo, indefinidamente. Pero entonces, el esquema permanece abierto, y la historia es posible. La filosofía de Platón, en su presentación y sus modelos, es por lo tanto inaugural, o mejor aún, aprovecha el momento inaugural.
Para retener este primer intento de explicación son las expulsiones y la purga. Por qué el parricidio del viejo padre Parménides, quien tuvo que formular, por primera vez, el principio de contradicción. Cabe señalar aquí de nuevo cómo dos oradores, adversarios irreconciliables, se ven obligados a unirse contra el mismo tercer hombre para que el diálogo siga siendo posible, para que el vínculo elemental de las relaciones humanas sea posible, para que la geometría sea posible. Cállate, no hagas ningún ruido, pon la cabeza en la arena, vete o muere. Extraña diagonal que se pensaba que era tan pura, y que es agonal y que sigue siendo una agonía.
El segundo intento contempla a Tales al pie de las pirámides, a la luz del sol. Involucra varios genes, uno de los cuales es ritual. (2) Pero no había tenido en cuenta el hecho de que las pirámides también son tumbas, que debajo del teorema de Tales, un cadáver fue enterrado, escondido. El espacio en el que interviene el geómetra es el espacio de las similitudes: está allí, evidente, al lado de tres tumbas de la misma forma y de otra dimensión: las tumbas se imitan entre sí. Y es el espacio puro de la geometría, el del grupo de similitudes que apareció con Thales. El resultado es que el teorema y su inmersión en la leyenda egipcia dice, sin decirlo, que yace debajo del operador mimético, construido concretamente y representado teóricamente, un cadáver real oculto. Había visto lo sagrado arriba, en el sol de Ra y en la epifanía platónica, donde el sol que había llegado en la idealidad del volumen estereométrico finalmente aseguró su diafanidad; No lo había visto debajo, escondido debajo de la lápida, en el cadáver incestuoso. Pero quedémonos en Egipto por un tiempo.
El tercer intento consiste en observar la doble escritura de geometría. (3) Usar figuras, esquemas y diagramas. Usando letras, palabras y oraciones del sistema, organizadas por su propia semántica y sintaxis. Leibniz ya había observado este doble sistema de escritura, consagrado por Descartes y por los pitagóricos, un doble sistema que se representa y se expresa uno por el otro. A veces le gustaba, como a muchos otros, privilegiar la intuición, clarividente o ciega, requerida por los primeros [diagramas] sobre las deducciones producidas por las segundas [palabras]. Hay, como es bien sabido, o como de costumbre, dos escuelas de pensamiento sobre el tema. Sucede que intercambian su poder a lo largo de la historia. También sucede que el esquema contiene más información que varias líneas de escritura, que estas líneas de escritura establecen indefinidamente lo que extraemos del esquema, como de un pozo o una cornucopia. El álgebra antigua escribe, dibujando línea por línea lo que la figura de la geometría antigua le dicta, lo que esa figura contiene de un solo golpe. El proceso nunca se detuvo; Todavía estamos hablando del cuadrado o de la diagonal. Ni siquiera podemos estar seguros de que la historia no sea precisamente eso.
Ahora, muchas historias informan que los griegos cruzaron el mar para educarse en Egipto. Demócrito lo dice; se dice de Tales; Platón lo escribe en el Timeo. Incluso, como de costumbre, había dos escuelas en desacuerdo sobre la cuestión. Uno sostenía que los griegos eran maestros de geometría; el otro, los sacerdotes egipcios. Esta disputa les hizo perder de vista lo esencial: que los egipcios escribieron en ideogramas y los griegos usaron un alfabeto. La comunicación entre las dos culturas puede considerarse en términos de la relación entre estos dos sistemas de escritura (signaletiques). Ahora, esta relación es exactamente la misma que la de la geometría que separa y une figuras y diagramas por un lado, y la escritura algebraica por el otro. ¿Son el cuadrado, el triángulo, el círculo y las otras figuras todo lo que queda de jeroglíficos en Grecia? Que yo sepa, son ideogramas. De ahí la solución: la relación histórica de Grecia con Egipto es pensable en términos de la relación de un alfabeto con un conjunto de ideogramas, y dado que la geometría no podría existir sin la escritura, las matemáticas se escriben en lugar de hablarse, esta relación se devuelve a la geometría como una operación que utiliza un doble sistema de escritura. Allí tenemos un pasaje fácil entre el lenguaje natural y el nuevo idioma, un pasaje que puede llevarse a cabo con la condición múltiple de que tengamos en cuenta dos idiomas diferentes, dos sistemas de escritura diferentes y sus lazos comunes. Y esto resuelve a su vez la cuestión histórica: el paro brutal de la geometría en Egipto, su congelamiento, su cristalización en ideogramas fijos y el desarrollo irrefrenable, en Grecia y en nuestra cultura, del nuevo lenguaje, ese discurso inagotable de las matemáticas. y rigor, que es la historia misma de esa cultura. La relación inaugural del ideograma geométrico con el alfabeto, las palabras y las oraciones se abre en un camino ilimitado.
Esta tercera solución borra una parte de los textos. El viejo sacerdote egipcio, en el Timeo, compara el conocimiento de los griegos cuando eran niños con la ciencia del tiempo de su propia cultura. (4) Evoca, para compararlos, inundaciones, incendios, fuego celestial, catástrofes . Ausentes de la solución están el sacerdote, la historia, ya sea mítica o real, en el espacio y el tiempo, la violencia de los elementos que oculta el origen y que, como dice claramente el Timeo, siempre oculta ese origen. Excepto, precisamente, del sacerdote, que conoce el secreto de esta violencia. El sol de Ra es reemplazado por Faetón, y la contemplación mística por la catástrofe de la desviación.
Debemos comenzar de nuevo, volver a esas líneas paralelas que nunca se encuentran. Por un lado, historias, leyendas y doxografías, compuestas en lenguaje natural. Por otro lado, todo un corpus, escrito en signos y símbolos matemáticos por geómetras, por aritméticos. Por lo tanto, no nos interesa simplemente vincular dos conjuntos de textos; debemos tratar de pegar, dos idiomas nuevamente juntos. La pregunta siempre surgió en el espacio de la relación entre la experiencia y lo abstracto, los sentidos y la pureza. Intenta averiguar el estado de lo puro, lo cual es impuro cuando cambia la historia. No. ¿Puedes imaginar (que existe) una Piedra Rosetta con algunas leyendas escritas en un lado, con un teorema escrito en el otro lado? Aquí no hay lenguaje desconocido o indescifrable, ningún lado de la piedra causa problemas; lo que está en cuestión es el borde común a los dos lados, su borde común; lo que está en cuestión es la piedra misma.
Leyendas Alguien u otro que concibió una nueva solución sacrificó un buey, un toro. El famoso problema de la duplicación del cubo surge con respecto a la piedra de un altar en Delos. Tales, en las Pirámides, está en el umbral de lo sagrado. Todavía no estamos, tal vez, en los orígenes. Pero, seguramente, lo que separa a los griegos de sus posibles predecesores, egipcios o babilonios, es el establecimiento de una prueba. Ahora, la primera prueba que conocemos es la prueba apagógica sobre la irracionalidad del radical 2. (5)
Y así, leyendas, una vez más. Elementos de Euclides, Libro X, primer escolio. Fue un pitagórico quien demostró, por primera vez, la llamada irracionalidad [de los números]. Quizás su nombre era Hippasus de Metapontum. Tal vez la secta había jurado no divulgar nada. Bueno, habló Hippasus de Metapontum. Quizás fue expulsado. En cualquier caso, parece seguro que murió en un naufragio. El anónimo scholiast continúa: «Los autores de esta leyenda querían hablar a través de la alegoría. Todo lo que es irracional y privado de forma debe permanecer oculto, eso es lo que intentaban decir. Que si alguna alma desea penetrar en esta región secreta y salir se abrirá, luego se verá envuelto en el mar del devenir, se ahogará en sus corrientes inquietas «.
Leyendas y alegorías y, ahora, historia. Porque leemos un evento significativo en tres niveles. Lo leemos en el scholia, comentarios, narraciones. Lo leemos en textos filosóficos. Lo leemos en los teoremas de la geometría. El evento es la crisis, la famosa crisis de los números irracionales. Debido a esta crisis, las matemáticas, en un punto extremadamente cercano a su origen, estuvieron muy cerca de morir. A raíz de esta crisis, el platonismo tuvo que ser refundido. La crisis tocó los logos. Si logos significa proporción, relación medida, lo irracional o alogon es la imposibilidad de medir. Si logos significa discurso, el alogon prohíbe hablar. Así, la exactitud se desmorona, la razón es muda.
Hippasus de Metapontum, u otro, muere de esta crisis, esa es la leyenda y su cobertura alegórica en el escolio de los Elementos. Parménides, el padre, muere de esta crisis: este es el sacrificio filosófico perpetrado por Platón. Pero, una vez más, la historia: Platón retrata a Theaetetus muriendo al regresar de la batalla de Corinto (369), Theaetetus, el fundador, precisamente, de la teoría de los números irracionales tal como se recapitula en el Libro X de Euclides. La crisis leída tres veces representa la lectura de una triple muerte: la legendaria muerte de Hippasus, el parricidio filosófico de Parménides, la muerte histórica de Theaetetus. Una crisis, tres textos, una víctima, tres narraciones. Ahora, en el otro lado de la piedra, en el otro lado y en otro idioma, tenemos la crisis y la posible muerte de las matemáticas en sí misma.
Dada entonces una prueba para explicar como lo haría un texto. Y, en primer lugar, la prueba, sin duda la más antigua de la historia, la que Aristóteles llamará reducción al absurdo. Dado un cuadrado cuyo lado AB = b, cuya diagonal AC = a:
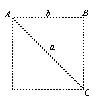
Deseamos medir AC en términos de AB. Si esto es posible, es porque las dos longitudes son mutuamente conmensurables. Entonces podemos escribir AC / AB = a / b. Se supone que a / b se reduce a su forma más simple, de modo que los enteros ayb son primos mutuos. Ahora, según el teorema de Pitágoras: a² = 2b². Por lo tanto, a² es par, por lo tanto a es par. Y si ayb son primos mutuos, b es un número impar. Si a es par, podemos plantear: a = 2c. En consecuencia, a² = 4c². En consecuencia, 2b² = 4c², es decir, b² = 2c². Por lo tanto, b es un número par.
La situación es intolerable, el número b es al mismo tiempo par e impar, lo que, por supuesto, es imposible. Por lo tanto, es imposible medir la diagonal en términos del lado. Son mutuamente inconmensurables. Repito, si logos es lo proporcional, aquí a / b o 1 / radical 2, el alogon es lo inconmensurable. Si logos es discurso o discurso, ya no puedes decir nada sobre la diagonal y el radical 2 es irracional. Es imposible decidir si b es par o impar. Hagamos una lista de las nociones utilizadas aquí. 1) ¿Qué significa que dos longitudes sean mutuamente conmensurables? Significa que tienen partes alícuotas comunes. Existe, o se podría hacer, una regla, dividida en unidades, en relación con la cual estas dos longitudes pueden, a su vez, dividirse en partes. En otras palabras, son otros cuando están solos juntos, cara a cara, pero son iguales, o casi, en relación con un tercer término, la unidad de medida tomada como referencia. La situación es interesante, y es bien conocida: dos entidades irreductiblemente diferentes se reducen a la similitud a través de un punto de vista exterior. Aquí es afortunado (o necesario) que el término medida tenga, tradicionalmente, al menos dos significados, el geométrico o metrológico y el significado de no desproporción, de serenidad, de no violencia, de paz. Estos dos significados derivan de una situación similar, una operación idéntica. Sócrates se opone a la crisis violenta de Callicles con el famoso comentario: ignoras la geometría. El tejedor real del estadista es el portador de una ciencia suprema: metrología superior, de la cual tendremos ocasión de hablar nuevamente. 2) ¿Qué significa que dos números sean primos mutuos? Significa que son radicalmente diferentes, que no tienen un factor común además de uno. De este modo, determinamos la primera situación, su otredad total, a menos que tengamos en cuenta la unidad de medida. 3) ¿Cuál es el teorema de Pitágoras? Es el teorema fundamental de medición en el espacio de similitudes. Porque es invariante por la variación de los coeficientes de los cuadrados, por la variación de las formas construidas en la hipotenusa y los dos lados del triángulo. Y el espacio de las similitudes es ese espacio donde las cosas pueden ser de la misma forma y de otro tamaño. Es el espacio de modelos y de imitaciones. El teorema de Pitágoras funda la medición en el espacio representativo de imitación. Pitágoras sacrifica un buey allí, repite una vez más el legendario texto. 4) ¿Qué es, ahora, la uniformidad? ¿Y qué es la rareza? Los términos en inglés reducen a una palabra los largos discursos griegos: incluso significa igual, unido, plano, igual; impar significa extraño, inigualable, extra, sobrante, desigual, en resumen, otro. Caracterizar un número por lo absurdo que es al mismo tiempo par e impar es decir que es al mismo tiempo igual y otro.
Conceptualmente, el teorema o prueba apagógica no hace más que jugar variaciones sobre la noción de igual y otro, usando la medición y la conmensurabilidad, usando el hecho de que dos números son primos mutuos, usando el teorema de Pitágoras, usando la uniformidad y la rareza. Es una prueba rigurosa, y la primera en la historia, basada en la mimesis. Dice algo muy simple: suponiendo mimesis, es reducible a lo absurdo. Así, la crisis de los números irracionales anula la aritmética pitagórica y el platonismo temprano.
Hippasus reveló esto, él muere por ello, al final del primer acto.
Hay que decir hoy que esto se dijo hace más de dos milenios. ¿Por qué seguir jugando un juego que se ha decidido? Porque es tan claro como mil soles que si la diagonal o el radical 2 son inconmensurables o irracionales, todavía pueden construirse en el cuadrado, que el modo de su existencia geométrica no es diferente del del lado. Incluso el joven esclavo de Meno, que es ignorante, sabrá cómo podrá construirlo. Del mismo modo, los niños saben cómo hacer trompos que la República analiza como estables y móviles al mismo tiempo. ¿Cómo es entonces que la razón puede tomar hechos que los niños más ignorantes saben cómo establecer y construir, y puede demostrar que son irracionales? Debe haber una razón para esta irracionalidad misma.
En otras palabras, estamos demostrando lo absurdo de lo irracional. Lo reducimos a lo contradictorio o indecidible. Sin embargo, existe; No podemos hacer nada al respecto. La parte superior gira, incluso si demostramos que, por razones inexpugnables, es, indecidiblemente, tanto móvil como fija. Esa es la forma en que está. Por lo tanto, toda la teoría que precede y funda la prueba debe ser revisada, transformada. No es la razón la que gobierna, es el obstáculo. Lo que se vuelve absurdo no es lo que hemos demostrado ser absurdo, es la teoría de la que depende la prueba. Aquí tenemos el movimiento muy común de la ciencia: una vez que llega a un callejón sin salida de este tipo, transforma inmediatamente sus presuposiciones.
Traducción: la mimesis es reducible a la contradicción o a lo indecidible. Sin embargo, existe; No podemos hacer nada al respecto. Gira Funciona, como dicen. Esa es la forma en que está. Siempre se puede demostrar que no podemos hablar ni caminar, o que Aquiles nunca alcanzará a la tortuga. Sin embargo, hablamos, caminamos, el Aquiles de patas flotantes sí pasa la tortuga. Esa es la forma en que está. Por lo tanto, toda la teoría que precede debe ser transformada. Lo que se vuelve absurdo no es lo que hemos demostrado ser absurdo, es la teoría en su conjunto de la que depende la prueba.
De ahí la (hola) historia que sigue. Theodorus continúa a lo largo del legendario camino de Hippasus. Multiplica las pruebas de irracionalidad. Él sube al radical 17. Hay muchos de estos absurdos, hay tantos de ellos como quieras. Incluso sabemos que hay muchos más que relaciones racionales. Con lo cual Theaetetus retoma el arcaico pitagorismo y da una teoría general que fundamenta, en una nueva razón, los hechos de la irracionalidad. El libro X de los elementos ahora se puede escribir. La crisis termina, las matemáticas recuperan un orden, Theaetetus muere, aquí termina esta historia, una técnica en el lenguaje del sistema, histórica en el lenguaje cotidiano que relata la batalla de Corinto. Platón reformula su filosofía, el padre Parménides es sacrificado durante el parricidio en el altar del principio de contradicción; porque seguramente lo Mismo debe ser Otro, después de una moda. Por lo tanto, se funda Royalty. El Royal Weaver combina en una red ordenada proporciones racionales y lo irracional; desapareció la crisis de la inversión, desapareció la tecnología de la dicotomía, fundada en el cuadrado, en la iteración de la diagonal. La sociedad, finalmente, está en orden. Este diálogo tiene un título fatal, no Geometría, sino el Estadista.
Se construye la piedra de Rosetta. Suponga que debe leerse en todos sus lados. En el lenguaje de la leyenda, en el de la historia, el de las matemáticas, el de la filosofía. El mensaje que entrega pasa de un idioma a otro. La crisis está en juego. Esta crisis es sacrificial. Una serie de muertes acompaña sus traducciones a los idiomas considerados. Tras estos sacrificios, reaparece el orden: en matemáticas, en filosofía, en historia, en sociedad política. El esquema de René Girard nos permite no solo mostrar el isomorfismo de estos lenguajes, sino también, y especialmente, su vínculo, cómo encajan entre sí. (6) Para que no sea suficiente narrar, los operadores de este movimiento deben estar hechos a aparecer. Ahora estos operadores, todos construidos en el par Same-Other, se ven, desplegados en su rigor, a lo largo de la primera prueba geométrica. así como el cuadrado equipado con su diagonal apareció, en mi primera solución, como el objeto tematizado de la relación intersubjetiva completa, la formación de la idealidad como tal, la prueba rigurosa aparece como tal, manipulando a todos los operadores de mimesis, a saber, el dinámica interna del esquema propuesto por Girard. El origen de la geometría está inmerso en la historia sacrifical y las dos líneas paralelas están en adelante conectadas. La leyenda, el mito, la historia, la filosofía y la ciencia pura tienen fronteras comunes sobre las cuales un esquema unitario construye puentes.
Metapontum y geómetra, él era el Pontifex, el Royal Weaver. Su muerte violenta en la tormenta, la muerte de Theaetetus en la violencia del combate, la muerte del padre Parménides, todas estas muertes son asesinatos. Lo irracional es mimético. La piedra que hemos leído era la piedra del altar en Delos. Y la geometría comienza en la violencia y en lo sagrado. (7)
Notas:
(1) La línea del altavoz 1 al altavoz 2 representa el canal de comunicación que une los dos altavoces. La línea de ruido al código o repertorio representa el vínculo indisoluble entre el ruido y el código. El ruido siempre amenaza con abrumar el código e interrumpir la comunicación. La comunicación exitosa, entonces, requiere la exclusión de un tercer término (ruido) y la inclusión de un cuarto (código). Ver «Diálogo platónico», capítulo 6 del ‘presente volumen. Ver también Michel Serres. Le Parasite (París: Grasset, 1980). -Ed.
(2) Ver «Matemáticas y filosofía: lo que vio Thales …… capítulo 8 del presente volumen. -Ed.
(3) Esta tercera explicación aparece como «Origine de la geometrie, 4» en Michel Serres, Hermes V.- Le Passage du Nord-Ouest (París: Minuit, 1980), pp. 175-84. -Ed.
(4) Platón, Timeo, 22 ter y sig.
(5) Una prueba apágica es aquella que procede al refutar la proposición que contradice la que se establecerá, en otras palabras, que procede por reductio ad absurduni. – Ed.
(6) La referencia es a la teoría de Rene Girard sobre la víctima emisaria. Ver capítulo 9, nota 9 en el presente volumen. – Ed.
(7) Es tan notable que la física de Epicuro, como la desarrolla Lucrecio en De Rerum Natura, se enmarca en el sacrificio de Ifigenia y la plaga de Atenas. Estos dos eventos, legendarios o históricos, se pueden leer usando la cuadrícula de fvsics. Pero, inversamente, toda esta física se puede leer usando el mismo esquema, ya que el término inane significa «purga» y «expulsión». He mostrado esto en detalle en La Naissance de la physique dans le texte de Luctice: Fleuves el turbulences (París: Minuit, 1977). (Ver también «Lucrecio: Ciencia y Religión», capítulo 9 del presente volumen. -Ed.)
Michel Serres
From ed. Harari, Josue V. And David F. Bell, Hermes; Literature, Science, Philosophy. the Johns Hopkins University Press, Baltimore, 1982



