Un triángulo escaleno es un triángulo en el que ninguno de los tres lados o los ángulos son iguales.
En la figura anterior, el número diferente de marcas y arcos indica que cada lado y ángulo del triángulo tiene una medida diferente. Esta es la notación de uso común en geometría; los lados que tienen la misma longitud (congruentes) se indican usando el mismo número de marcas de graduación, y los ángulos que son iguales se indican usando el mismo número de arcos.
Propiedades de los triángulos escalenos
Hay algunas propiedades que comparten todos los triángulos:
- La suma de todos los ángulos internos de un triángulo es igual a 180 °.
- La longitud del lado de un triángulo corresponde al tamaño del ángulo opuesto al lado; cuanto más largo sea el lado, mayor será el ángulo. Vale la pena señalar que las proporciones no se corresponden: si el lado a tiene el doble de longitud que b , no significa que el ángulo A tiene el doble del tamaño del ángulo B.
- La suma de la longitud de dos lados de un triángulo es mayor que la longitud del tercer lado.
Hay más propiedades que comparten todos los triángulos, pero estas son algunas propiedades de uso común en geometría.
Los triángulos escalenos tienen específicamente las siguientes propiedades:
- Sin lados iguales.
- No hay ángulos iguales.
- Sin eje de simetría: un triángulo escaleno no se puede dividir en dos mitades idénticas. En contraste, los triángulos equiláteros e isósceles tienen líneas de simetría.
- Los triángulos escalenos pueden ser triángulos rectángulos, triángulos obtusos o triángulos agudos.
Área y perímetro
Hay varias formas diferentes de encontrar el área de un triángulo. La fórmula general para el área (A) de un triángulo es
donde b es la base y h es la altura del triángulo. Esto funciona para cualquier triángulo dado que la información proporcionada permite encontrar la base y la altura del triángulo.
Para los triángulos escalenos, dado que cada lado tiene una longitud diferente, en la mayoría de los casos el problema probablemente proporcionará las longitudes de los lados o hará posible encontrar las longitudes de los lados. En los casos en los que se conoce cada lado de un triángulo, la fórmula de Heron se puede usar para encontrar el área del triángulo:
En la fórmula de Heron, a, byc representan las longitudes de los lados del triángulo, y s es:
Tenga en cuenta que a, byc están etiquetados arbitrariamente en el triángulo. Cualquiera de los lados se puede etiquetar como a, bo c. También se puede hacer referencia al triángulo de arriba para encontrar el perímetro de un triángulo. Para encontrar el perímetro (P) de un triángulo, simplemente encuentra la suma de la longitud de cada lado del triángulo:
P=a + b + c
Triángulos categorizados por sus lados
Los triángulos a menudo se clasifican por sus lados o ángulos. Un triángulo escaleno es uno de los tres triángulos clasificados por sus lados.
| Tipo | Lados | Figura |
|---|---|---|
| Escaleno | ningún lado tiene la misma longitud |  |
| Isósceles | 2 lados tienen la misma longitud | 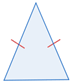 |
| Equilateral | todos los lados tienen la misma longitud | 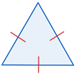 |
Los triángulos también se suelen clasificar como obtusos , agudos o triángulos rectángulos según sus ángulos.



