Un triángulo es un polígono con tres lados y tres ángulos .
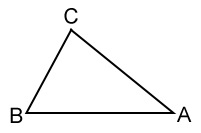
Los tres lados del triángulo ABC que se muestran arriba, escritos simbólicamente como △ ABC, son segmentos de línea AB, BC y AC. Un vértice se forma cuando dos lados de un triángulo se cruzan. △ ABC tiene vértices en A, B y C. Se forma un ángulo interior en cada vértice. Los ángulos A, B y C son los tres ángulos interiores de △ ABC.
Un segmento de línea desde el vértice de un triángulo hasta el lado opuesto al vértice y es perpendicular al lado opuesto se llama altitud. El lado que es perpendicular a la altitud se llama base del triángulo. En el triángulo ABC a continuación, el segmento de línea CD es una altitud y el lado AB es una base.
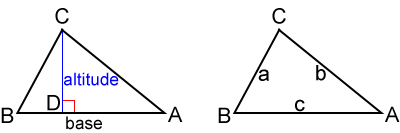
Es común nombrar los lados de un triángulo en función de su ángulo opuesto. Esto a menudo implica el uso de letras mayúsculas y minúsculas para nombrar un ángulo y su lado opuesto. Consulte △ ABC anterior como ejemplo. El lado BC es opuesto al ángulo A, por lo que está etiquetado como lado a.
Suma de ángulos
Usando propiedades de líneas paralelas y ángulos alternos internos, podemos mostrar que la suma de los ángulos internos de un triángulo es 180 °.
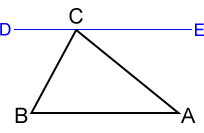
- Para △ ABC que se muestra arriba, deje que la línea DE, que contiene el vértice C, sea paralela al lado AB. Dado que ∠DCE es un ángulo recto, ∠ECA + ∠DCB + ∠BCA=180 °.
- Además, dado que DE es paralelo a AB, esto forma dos conjuntos de ángulos internos alternos congruentes tales que ∠ECA≅∠A y ∠DCB≅∠B.
- Sustituyendo los ángulos A y B en nuestra ecuación anterior, ∠A + ∠B + ∠BCA=180 °, donde ∠BCA=∠C.
Ángulos exteriores
Para un triángulo, un ángulo exterior es un ángulo formado por un lado del triángulo y una línea que se extiende desde otro de sus lados. La medida de un ángulo exterior de un triángulo es igual a la suma de sus dos ángulos interiores remotos.
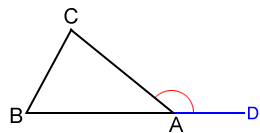
Para △ ABC que se muestra arriba, ∠CAD es el ángulo exterior para ∠A y ∠B y ∠C son los dos ángulos interiores remotos. Sabemos que ∠CAB + ∠B + ∠C=180 °. Además, ∠CAB y ∠CAD forman un ángulo recto, por lo que ∠CAB + ∠CAD=180 °. Dado que ambas sumas son iguales a 180 °:
∠CAB + ∠CAD=∠CAB + ∠B + ∠C
∠CAD=∠B + ∠C
Lo mismo se puede mostrar para cualquier ángulo exterior de cualquier triángulo.
Clasificación de triángulos
Los triángulos a menudo se clasifican por sus ángulos y lados, como se muestra en las tablas a continuación.
Por ángulos:
| Tipo | Ángulos | Figura |
|---|---|---|
| Agudo | todos los ángulos interiores & lt; 90 ° | 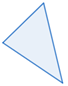 |
| Obtuso | 1 ángulo interior & gt; 90 ° |  |
| Derecha | 1 ángulo=90 ° |  |
| Equiangular | cada ángulo interior=60 ° | 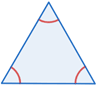 |
Por lados:
| Tipo | Lados | Figura |
|---|---|---|
| Scalene | no hay 2 lados congruentes |  |
| Isósceles | 2 lados congruentes | 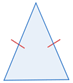 |
| Equilateral | todos los lados son congruentes | 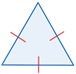 |
Comparar lados y ángulos
Un triángulo solo se puede formar cuando la suma de cualquiera de los dos lados del triángulo es mayor que su tercer lado.
Ejemplo:
Los lados de △ ABC son a=4, b=6 y c=9. ¿Se puede formar un triángulo con los lados dados?
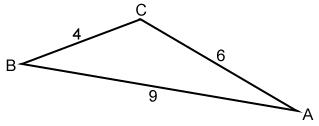
Dado que 4 + 6 & gt; 9, 4 + 9 & gt; 6 y 6 + 9 & gt; 4 podemos formar △ ABC. Esto solo nos dice que un triángulo puede estar formado por los tres lados dados. No clasifica el triángulo.
Si un lado de un triángulo es más largo que otro lado, el ángulo opuesto al lado más largo debe ser mayor que el ángulo opuesto al lado más pequeño. Esto es cierto para cualquier triángulo.
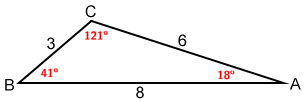
Como ejemplo, puede ver desde las medidas de los lados y ángulos dadas para △ ABC arriba, AB & gt; ANTES DE CRISTO. En base a esto, sabemos que ∠C & gt; ∠A.
Por el contrario, cuanto mayor sea la medida del ángulo, mayor será la longitud del lado opuesto. Dado que ∠B & gt; ∠A, AC & gt; BC.



