Un triángulo es un polígono de tres lados que tiene un ángulo interior en cada uno de sus vértices . Los triángulos a menudo se clasifican por sus ángulos o lados .
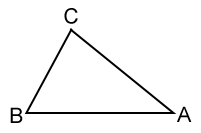
El triángulo △ ABC, que se muestra arriba, tiene lados AB, BC y AC, y ángulos A, B y C, formados en los vértices A, B y C.
Triángulos clasificados por sus ángulos
La siguiente tabla muestra los tipos de triángulos clasificados por sus ángulos.
| Tipo | Ángulos | Figura |
|---|---|---|
| Agudo | todos los ángulos interiores & lt; 90 ° | 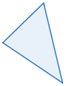 |
| Obtuso | 1 ángulo interior & gt; 90 ° |  |
| Derecha | 1 ángulo=90 ° |  |
| Equiangular | cada ángulo interior=60 ° | 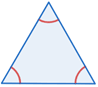 |
Triángulos clasificados por sus lados
La siguiente tabla muestra los tipos de triángulos clasificados por sus lados.
| Tipo | Lados | Figura |
|---|---|---|
| Scalene | no hay 2 lados congruentes |  |
| Isósceles | 2 lados congruentes | 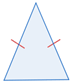 |
| Equilateral | todos los lados son congruentes | 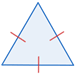 |
Usando el Teorema de Pitágoras para clasificar triángulos por sus ángulos
Cuando uno de los ángulos de un triángulo es un ángulo recto , el triángulo es un triángulo rectángulo. Las longitudes de los tres lados de un triángulo rectángulo siguen el Teorema de Pitágoras . El Teorema de Pitágoras también se puede utilizar para clasificar triángulos por ángulos de la siguiente manera:
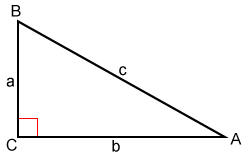
Para △ ABC, dado que el lado c es el lado más largo:
- Si c 2 =a 2 + b 2 , entonces △ ABC es un triángulo rectángulo con ángulo recto C.
- Si c 2 & gt; a 2 + b 2 , entonces △ ABC es un triángulo obtuso con ángulo obtuso C.
- Si c 2 & lt; a 2 + b 2 , entonces △ ABC es un triángulo agudo con todos los ángulos agudos.
Ejemplo:
Clasifica un triángulo cuyos lados tengan longitudes de 3, 6 y 8.
Dado que 8 es la longitud de lado más grande, sea c=8, a=3 y b=6:
| c 2 =8 2 =64 |
| a 2 + b 2 =3 2 +6 2 =9 + 36=45 |
Desde 64 & gt; 45, c 2 & gt; a 2 + b 2 , entonces el triángulo es un triángulo obtuso.



