La teoría de conjuntos es una rama de las matemáticas que estudia conjuntos. Los conjuntos son una colección de objetos (normalmente) bien definidos. A continuación se muestran algunos ejemplos:
- {a, b, c, d, e}
- {n | n ∈ ℕ, 1 ≤ n ≤ 10}
- {verde, rojo, azul, amarillo, blanco, negro, violeta}
- El diagrama de Venn muestra un conjunto compuesto por frutas y verduras.
Tenga en cuenta que un conjunto puede estar formado por prácticamente cualquier tipo de objeto. Si bien esto es cierto, la teoría de conjuntos se ocupa principalmente de objetos que son relevantes para las matemáticas. Los objetos de un conjunto se denominan elementos. Por ejemplo, en el diagrama de Venn, cada fruta o verdura es un elemento de su conjunto respectivo, y tanto las verduras como las frutas son parte del conjunto universal . La porción central donde se cruzan el conjunto de frutas y verduras contiene solo tomates, que se consideran una fruta botánicamente, pero comúnmente se consideran una verdura en el contexto de la cocción. Este tipo de relaciones son la base de la teoría de conjuntos básica.
Notación y conceptos básicos de la teoría de conjuntos
En su nivel más básico, la teoría de conjuntos describe la relación entre objetos y si son elementos (o miembros) de un conjunto dado. Los conjuntos también son objetos y, por lo tanto, también se pueden relacionar entre sí normalmente mediante el uso de varios símbolos y notaciones.
Aunque la teoría de conjuntos puede parecer arbitraria y no necesariamente útil por sí sola, se usa en todas las matemáticas y se puede considerar como un bloque de construcción fundamental. Muchos conceptos matemáticos serían difíciles de definir con precisión (y concisión) sin el uso de la teoría de conjuntos. Como tal, es importante estar familiarizado con los diversos símbolos y notaciones que se utilizan en la teoría de conjuntos para comprender y comunicar conceptos matemáticos de manera eficaz. La siguiente tabla incluye algunos de los símbolos más comunes.
| Símbolo | Definición/significado | Ejemplo |
|---|---|---|
| {} | Indica una colección de elementos | {1, 3, 7, 9} |
| ∅ | Conjunto vacío : el conjunto no contiene elementos | {} |
| … | Indica que el conjunto continúa el patrón en la dirección correspondiente hacia el infinito negativo (izquierda) o positivo (derecha) | {…, -9, -7, -3, -1, 1, 3, 7, 9, …} |
| | | «Tal que» | a∈ℤ | a & gt; 3 – «a es un número entero tal que a es mayor que 3» |
| ∩ | «y» o «intersección» | A={1, 2, 3, 4} B={4, 5, 6} A ∩ B={4} |
| ∪ | «o» o «unión» | A={1, 2, 3, 4} B={4, 5, 6} A ∪ B={1, 2, 3, 4, 5, 6 } |
| ⊆ | Subconjunto : A es un subconjunto de B si todos sus elementos están incluidos en B | {1, 2} ⊆ {1, 2, 3, 4, 5} {1, 2, 3, 4, 5} ⊆ {1, 2, 3, 4, 5 } |
| ⊂ | Subconjunto adecuado/estricto : A es un subconjunto adecuado de B si A es un subconjunto de B, pero no es igual a B | {1} ⊂ {1, 2, 3, 4, 5} {1, 2} ⊂ {1, 2, 3, 4, 5} {1, 2 , 3} ⊂ {1, 2, 3, 4, 5} {1, 2, 3, 4} ⊂ {1, 2, 3, 4, 5} |
| ∈ | Elemento de : indica que el objeto a la izquierda del símbolo es un elemento del objeto a la derecha | x∈ℚ – «x es un elemento de los números racionales» |
| Conjunto universal : el conjunto de todos los valores posibles | A={1, 2} B={3, 4, 5} ={1, 2, 3, 4, 5} | |
| A c o A ‘ | Complemento : todos los elementos que no están en el conjunto A | ={1, 2, 3, 4, 5} A={1, 2, 3} A c ={4,5 } |
| [a, b] | Intervalo cerrado : valores entre ayb, incluidos ayb | [1,4]={1, 2, 3, 4} si solo incluye números enteros |
| (a, b) | Intervalo abierto : valores entre ayb sin incluir ayb | (1,4)={2, 3} si solo incluye números enteros |
| | A | | Orden/cardinalidad – número de elementos en el conjunto | A={3, 6, 7, 9} | A |=4 |
| ℕ | Números naturales : solo números positivos sin decimales ni fracciones | {1, 2, 3, …} |
| ℤ | Enteros : todos los números positivos y negativos sin decimales ni fracciones, incluido 0 | {…, -3, -2, -1, 0, 1, 2, 3, …} |
| ℚ | Números racionales : un número que se puede representar como una fracción compuesta por números enteros | ⅔ |
| ℝ | Números reales : números racionales y números irracionales | π, e , 3, ½, 0.25 |
| ℂ | Números complejos : números formados por un componente real e imaginario | 4 + 2ⅈ |
Orden e igualdad de conjuntos
El orden de un conjunto se refiere al tamaño de un conjunto. También se conoce como cardinalidad del conjunto. Los conjuntos pueden tener un orden finito o infinito. Si un conjunto tiene un orden finito, el orden de un conjunto está determinado por el número de elementos en el conjunto. Por ejemplo, el conjunto A={1, 2, 5, 7, 9} tiene un orden de 5, ya que contiene 5 elementos. Usando la notación de conjuntos, podríamos expresar el orden de A como:
| A |=4
Tenga en cuenta que el orden de los elementos en un conjunto no importa. Por ejemplo, dados los conjuntos
A={1, 2, 5, 7, 9}
B={1, 5, 2, 9, 7}
Diríamos que A y B son conjuntos iguales, o A=B. Esto se debe a que la igualdad de conjuntos está determinada por los elementos dentro del conjunto, no por el orden en que se enumeran los elementos.
Ejemplo
Dados los conjuntos
A={5, 3, 1}
B={3, 1, 5, 13, 10,}
C={2, 10, 6, 4}
consulte la tabla según sea necesario y determine los resultados de las siguientes operaciones:
- A ∩ B
- A ∩ C
- B ∪ C
i. A ∩ B={1, 3, 5}
- Debido a que todos los elementos de A también están en B, también podemos decir que A es un subconjunto propio de B, o A ⊂ B. Además, | A |=3 y | B |=5.
ii. A ∩ C=∅
- A y C no tienen elementos comunes, por lo que su intersección es un conjunto vacío. También podemos decir que A y B son conjuntos mutuamente excluyentes.
iii. B ∪ C={1, 2, 3, 4, 5, 6, 10, 13}
- La unión de B y C es el conjunto que contiene todos los elementos de B y C.
Conjuntos infinitos
Los conjuntos pueden ser finitos o infinitos. Además, los conjuntos infinitos pueden ser contables o incontables.
Contable
Cualquier conjunto infinito que pueda emparejarse con los números naturales en una correspondencia uno a uno, de modo que cada uno de los elementos del conjunto pueda identificarse uno a la vez es un conjunto infinito numerable. Por ejemplo, dado el conjunto
{0, -1, 1, -2, 2, -3, 3, …}
sus elementos se pueden emparejar con un número natural de la siguiente manera:
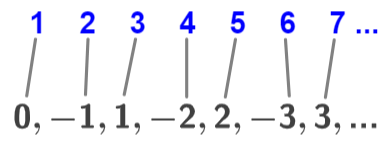
Por lo tanto, es posible identificar el elemento n como el número natural n .
Incontable
Los conjuntos innumerables no se pueden organizar de la misma manera que los conjuntos infinitos contables. El conjunto de números reales de cero a uno, o (0, 1), no es contable porque no es posible emparejar cada uno de los elementos del conjunto con un elemento único en el conjunto de números naturales. Por ejemplo, sea {0, x 1 , x 2 , …, 1} el conjunto de números reales de cero a uno donde x 1 ≠ x 2 . La figura siguiente muestra que los elementos no se pueden mapear de la misma manera que la figura anterior (con conjuntos infinitos contables):
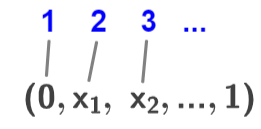
Los números naturales se pueden asignar a los elementos, como se muestra en la figura, pero debido a que hay números reales entre dos números reales distintos, no hay números naturales para asignar a los números reales entre 0 y x 1 , x 1 y x 2 , y así sucesivamente. Por lo tanto, el conjunto es incontablemente infinito.
Establecer operaciones
Algunas de las operaciones básicas de conjuntos (unión e intersección) se discutieron anteriormente. A continuación se muestran algunas otras operaciones.
Producto cartesiano
El producto cartesiano de A y B, denotado A × B, es el conjunto compuesto por todos los pares ordenados (a, b) de manera que a es un elemento de A y b es un elemento de B. Usando set-builder notación, esto se puede denotar como:
Tenga en cuenta que el orden en el que se escriben los seis elementos del conjunto no importa, pero sí el orden de los pares ordenados. Por ejemplo, (a, i) no es el mismo par ordenado que (i, a). Generalmente, si hay m elementos en A y n elementos en B, hay m · n elementos en A × B.
Conjunto de energía
Un conjunto de potencias es un conjunto que se compone de todos los posibles subconjuntos de un conjunto. Sea A={1, 2, 3}. El conjunto de potencias de A, denotado ℘ (A), es:
℘ (A)={{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Observe que tanto el conjunto vacío como el conjunto A se consideran subconjuntos de A. En general, si hay n elementos en A, hay 2 n subconjuntos en ℘ (A).
Leyes de De Morgan
En la teoría de conjuntos, las leyes de De Morgan son un conjunto de reglas que relacionan la unión y la intersección de conjuntos a través de sus complementos.
Unión de conjuntos:
El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos:
(A ∪ B) C =A C ∩ B C
Dado que A y B son subconjuntos del conjunto universal , esta relación se puede ver en la siguiente figura:
La unión de A y B, A ∪ B, está sombreada en azul. Su complemento, (A ∪ B) C está sombreado en amarillo. La intersección de los complementos de A y B, A C ∩ B C también está sombreada en amarillo.
Intersección de conjuntos:
El complemento de la intersección de dos conjuntos es igual a la unión de sus complementos:
A ∩ B=A C ∪ B C
Dado que A y B son subconjuntos del conjunto universal , esta relación se puede ver en la siguiente figura:
La intersección de A y B, A ∩ B, está sombreada en rojo. Su complemento, (A ∩ B) C está sombreado en gris. La unión de los complementos de A y B, A C ∪ B C , también está sombreada en gris.



