Los Elementos de Euclides se trata de la obra más importante de Euclides, que encontramos dividida en 13 libros. Los 6 primeros libros hablan específicamente sobre la geometría plana, mientras que los 3 siguientes solamente se centran en la teoría de números, el décimo en inconmensurables y los tres últimos en geometría de sólidos.
Todos estos estudios son fundamentales para comprender el conocimiento y obra que Euclides trataba de dar a ofrecer. Aunque con el tiempo han sufrido alguna modificaciones observamos en estos estudios la referencia al teorema de Euclides.
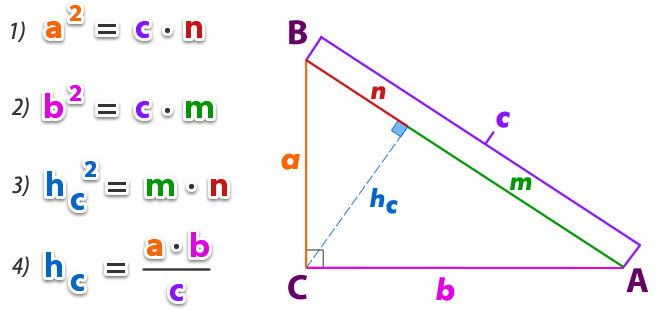
Teorema de Euclides referido a la altura
El primer caso que se muestra que forma el teorema de Euclides se refiere a un triángulo rectángulo. Nos referimos a la altura dibujada desde un ángulo recto y es la razón geométrica media, significa que ser refiere a la altura del cuadrado. La altura entre los segmentos de línea suele estar determinada por la hipotenusa. Puedes observar la explicación en la imagen del rectangulo.
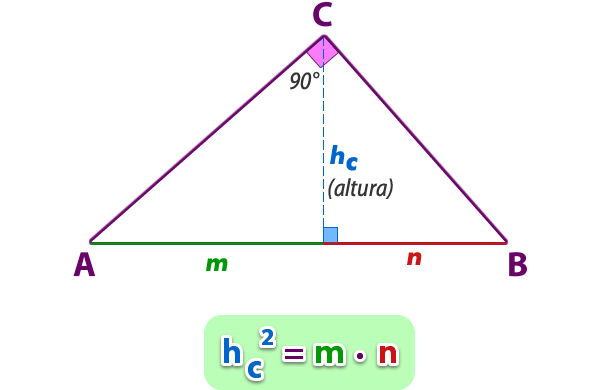
Teorema de Euclides referido al cateto
Para poder entender el Teorema de Euclides se necesitan ejemplos y practica. Cuando se hace referencia al cateto, partimos de un triángulo rectángulo donde nos obliga a despejar m y n se refiere a los catetos. Se tiene que remplezar la altura, la cual se obtiene desde el ángulo recto. Es el producto de los catetos entre la hipotenusa.
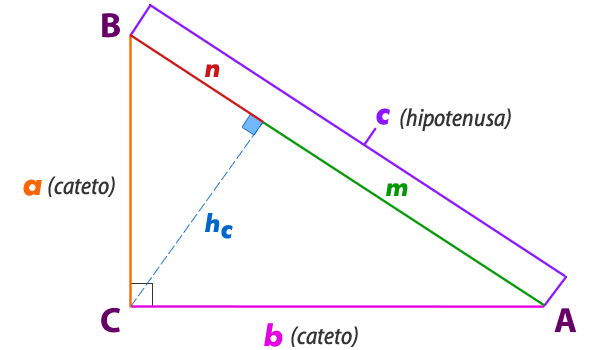
Aplicando el Teorema de Euclides nos permite llegar con la siguiente formula;
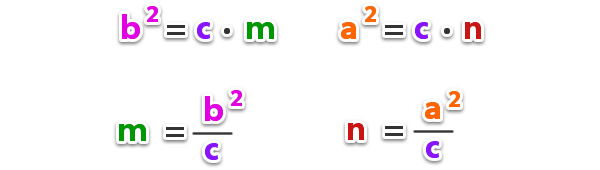
La relación que vemos entre los teoremas de Euclides
Ya hemos entendido la parte más importante del teorema de Euclides, debemos entender que los teoremas de altura y catetos tienen una relación entre sí. Esto se debe a que la medida de ambos esta condicionada respecto a la hipotenusa del triángulo rectángulo.
Si se tiene en cuenta esta parte es necesario entender que usando los teoremas de Euclides podemos obtener el valor de la altura. Esto lo podemos conseguir despejando los valores de m y n del teorema de los catetos y se puedan reemplazar en el teorema de la altura. Así que observamos que la altura es igual a la multiplicación de los catetos divididos entre la hipotenusa. Entonces, aplicamos lo siguiente;
- b2 = c * m
- m = b2 ÷ c
- a2 = c * n
- n =a2 ÷ c
Como se ha mencionado, en el teorema de la altura se reemplazan los valores de m y n. Esto quedará entonces de la siguiente manera:
- hc2 = m * n
- hc2 = (b2 ÷ c) * (a2 ÷ c)
- hc = (b2 * a2) ÷ c
Ejercicio con solución
Si tenemos un triángulo determinado ABC como el siguiente, el cual el rectángulo en A va a determinar la medida de AC y AD. Los datos que se cuentan son AB= 30 cm y BD= 18 cm. A partir de estos datos podemos realizar los cálculos pertinentes para obtener al resultado.
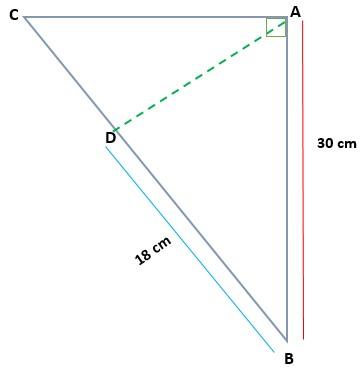
Solución
Entre otras cosas, requiere algo de pensamiento matemático. Medimos una de los costados de proyección en BD y uno de los catetos originales en AB. Luego, debemos encontrar el valor correspondiente a BC. Esta idea ya existe y ahora debe implementarse utilizando la fórmula proporcionada por el teorema de Euclides. Para ello, se debe explicar lo siguiente:
- AB2 = BD * BC
- (30)2 = 18 * BC
- 900 = 18 * BC
- BC = 900 ÷ 18
- BC = 50 cm
Después de esto el valor del cateto CD va a poder ser encontrado, debido a que se tiene el valor del cateto BC= 50 cm. Se da por entendido de que no se trata de nada tan complicado hasta este momento. Por lo que se deberá hacer lo siguiente:
- CD = BC – BD
- CD = 50 – 18 = 32 cm
Una vez que se ha encontrado el valor de CD, también es posible que se pueda encontrar el valor del cateto AC, para esto se aplica de nuevo el teorema:
- AC2 = CD * BD
- AC2 = 32 * 50
- AC2 = 160
- AC = √1600 = 40 cm
Se puede determinar el valor de la altura AD mediante el teorema de la altura, el cual se usa los catetos CD y BD que han sido proyectados y son conocidos:
- AD2 = 32 * 18
- AD2 = 576
- AD = √576
- AD = 24 cm



