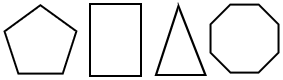
Un polígono es una figura plana cerrada formada por tres o más líneas mensajes . Los siguientes son algunos ejemplos.
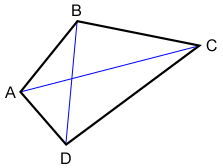
Los segmentos de línea que forman un polígono se llaman lados. Dos lados conectados forman un ángulo en un punto llamado vértice. Una diagonal es un segmento de línea que une dos vértices no consecutivos. En el siguiente polígono, , , y son cuatro lados. Forman cuatro ángulos: ∠A, ∠B, ∠C y ∠D. y son dos diagonales.
Hay muchas formas de clasificar polígonos; los siguientes son algunos de ellos.
Polígonos regulares e irregulares
Polígono regular
Un polígono regular es un polígono en el que todos los lados tienen la misma longitud (equilátero) y todos los ángulos tienen la misma medida (equiangular). A continuación se muestran algunos ejemplos.
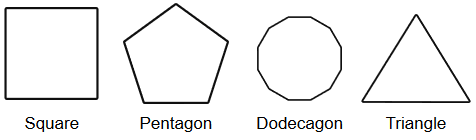
Polígono irregular
Un polígono irregular tiene lados o ángulos que no son congruentes, como se muestra a continuación.
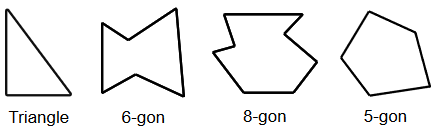
Polígonos convexos y cóncavos
Los polígonos se pueden clasificar como convexos o cóncavos.
Polígono convexo
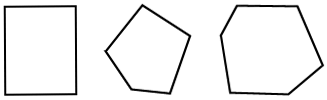
Si todos los ángulos interiores de un polígono son menores de 180 °, es convexo. Un polígono regular siempre es convexo. Los siguientes son algunos ejemplos.
Polígono cóncavo
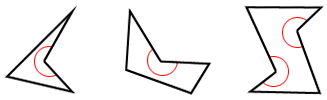
Si uno o más ángulos interiores de un polígono son mayores de 180 °, es cóncavo. Un polígono cóncavo es siempre un polígono irregular. Los siguientes son unos cuantos ejemplos. Los ángulos interiores mayores de 180 ° están marcados con un arco rojo.
Clasificación de polígonos por su número de lados
Los polígonos se clasifican comúnmente según la cantidad de lados que tienen. En general, un polígono con n-número de lados se llama n-gon. Algunos polígonos importantes tienen nombres específicos, como triángulos, pentágonos, hexágonos, etc. Los siguientes son algunos ejemplos.
| Polígono | # de lados | Forma |
|---|---|---|
| Triángulo | 3 |  |
| Cuadrilátero | 4 |  |
| Pentágono | 5 |  |
| Hexagon | 6 |  |
| Octágono | 8 |  |
Hay muchos otros polígonos, y cada uno de los polígonos anteriores puede clasificarse mejor. Por ejemplo, un triángulo puede clasificarse además como agudo , obtuso o triángulo rectángulo . Obtenga más información sobre estos polígonos navegando por este sitio web.



