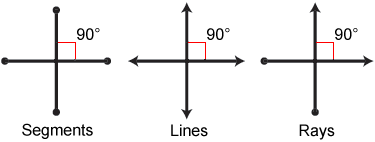
El término «perpendicular» significa encontrar o cruzar en ángulos rectos . Líneas , rayos , segmentos de línea y < un href=""/ plane">planos puede ser perpendicular.
Las líneas perpendiculares, los rayos y los segmentos de línea son líneas o partes de líneas que se encuentran o se cruzan en ángulos rectos.
Si las líneas lym son perpendiculares entre sí, podemos escribir l⊥m donde «⊥» es el símbolo de perpendicular.
Reglas que involucran líneas perpendiculares
Las líneas perpendiculares crean propiedades y relaciones interesantes en geometría, las siguientes son algunas de ellas:
• Un triángulo es un triángulo rectángulo si 2 lados del triángulo son perpendiculares.
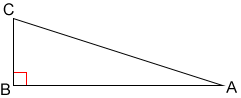
En el diagrama anterior, el triángulo ABC es un triángulo rectángulo con un ángulo recto en el vértice B porque los lados AB y BC son perpendiculares.
• En geometría plana, solo puede haber una línea dibujada a través de un punto dado, no en una línea dada que sea perpendicular a la línea dada. Esto se conoce como el postulado perpendicular.
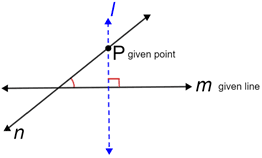
En el diagrama anterior, solo la línea l se puede trazar a través del punto P que es perpendicular a la línea m. Cualquier otra línea trazada a través de P, como la línea n en el diagrama, no será perpendicular a la línea m.
• La distancia desde un punto que no está en una línea a la línea es la longitud del segmento de línea perpendicular desde el punto a la línea. También es la distancia más corta desde el punto hasta la línea.
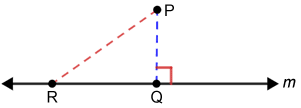
En el diagrama anterior, la distancia de P am es la longitud del segmento ya que es perpendicular am. Observe que el segmento también es una distancia medible de P am, pero no la distancia medible más corta, ya que no es perpendicular am.
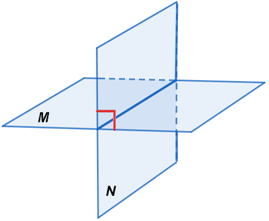
• Dos planos que se cruzan en ángulo recto son perpendiculares entre sí.
• Una línea se llama bisectriz perpendicular de un segmento de línea si es perpendicular al segmento y corta el segmento en 2 partes iguales.
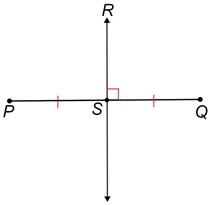
En el diagrama anterior, es la bisectriz perpendicular de desde es perpendicular a y ≅ .
• La altitud de un triángulo es el segmento de línea perpendicular desde un vértice hasta el lado opuesto o la línea que contiene el lado opuesto de un triángulo.
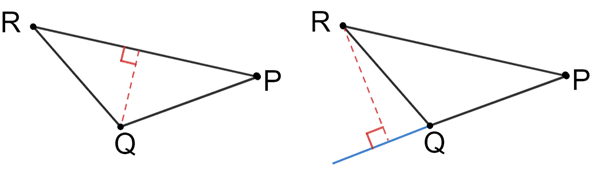
En el diagrama anterior, los segmentos punteados perpendiculares desde el vértice Q al lado PR y desde el vértice R al lado PQ son ambas altitudes para el triángulo PQR.
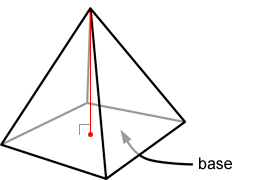
• La altura de una pirámide es el segmento de línea perpendicular desde la base de la pirámide hasta su vértice.
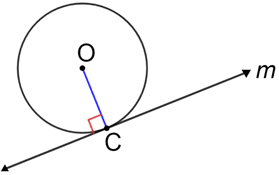
• Una línea tangente a un círculo es perpendicular al radio del círculo que se encuentra con la línea en el punto de tangencia.