El mayor factor común (MCD) de dos o más números es el factor más grande que comparten. El máximo factor común se puede encontrar utilizando varios métodos, como enumerar factores, utilizar la factorización prima o el algoritmo de Euclides, entre otros. El MCD de dos números, como 12 y 16, se puede denotar como MCD (12, 16).
En el caso de números más pequeños, enumerar los factores no suele ser demasiado difícil y resulta útil para encontrar el mayor factor común.
Enumerar factores para encontrar el MCD
Para encontrar el máximo factor común de 8 y 12 :
Primero: enumere los factores
| Factores de 8: | 1, 2, 4, 8 |
| Factores de 12: | 1, 2, 3, 4, 6, 12 |
A continuación: compare estos factores e identifique el factor más grande que comparten los dos números
| El mayor factor común de 8 y 12 es 4 . |
| Esto también se puede escribir como GCF (8, 12 ) =4 . |
Uso de factorización prima para encontrar el MCD
Para encontrar el máximo factor común de 36 y 48 ,
Primero: encuentre la factorización prima
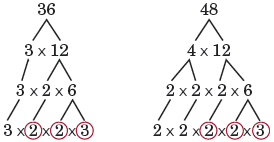
Los números 36 y 48 tienen los factores primos 2 , 2, y 3 en común.
Siguiente: multiplique estos factores primos: 2 × 2 × 3=12
GCF (36, 48 ) =12
Saber cómo encontrar el máximo factor común es útil para expresar fracciones comunes en su forma más simple.
Usando el algoritmo de Euclid para encontrar el MCD
La factorización prima y la enumeración de factores para encontrar el MCD pueden volverse tediosos rápidamente a medida que aumentan los números. El algoritmo de Euclid para encontrar el GCF es uno de varios algoritmos más eficientes para encontrar el GCF.
El algoritmo de Euclides es un algoritmo que involucra una división larga que se basa en el principio de que el MCD de dos números no cambia si el número más grande se reemplaza con su diferencia con el número más pequeño. Entonces, GCF (18, 34) es lo mismo que GCF (34-18, 18) o GCF (16, 18). No entraremos en detalles para demostrar por qué funciona el algoritmo euclidiano, pero para usar el algoritmo para encontrar el GCF, siga estos pasos:
- Divida el número más grande por el número más pequeño. Si el resto es 0, el divisor es el MCD. De lo contrario, continúe con el siguiente paso.
- Divida el número más pequeño (el divisor anterior) por el resto. Si el nuevo resto es 0, el divisor es el MCD.
- Continúe el proceso de dividir el divisor anterior por el resto hasta que no quede resto. El divisor que da como resultado un resto de 0 es el MCD de los dos números originales.
Ejemplo
Busque GCF (114, 288):
Tenga en cuenta que el cociente realmente no importa para este algoritmo, y no estamos completando el problema de división larga original real.
Después de dividir 4 veces, el resto es 0 y el último divisor es 6. Por lo tanto, según el algoritmo, GCF (114, 288)=6. Esto se puede probar dividiendo 114 y 288 por 6:
114 ÷ 6=19
288 ÷ 6=48
19 y 48 no comparten ningún factor común, lo que confirma que 6 es el MCD de 114 y 288.
Este algoritmo también se puede utilizar para encontrar el MCD de más de 2 números al encontrar el MCD entre los dos primeros números y luego calcular el MCD del resultado y el siguiente número. Esto se puede escribir como:
GCF (a, b, c)=GCF (GCF (a, b), c)



