Matemáticas primarias, también conocidas como matemáticas elementales o matemáticas tempranas, es una categoría de matemáticas que cubre temas que normalmente se aprenden en la educación temprana. Los temas aprendidos en matemáticas de primaria, incluidas las herramientas, los conceptos, etc., proporcionan una base para el aprendizaje de las matemáticas. Incluyen temas como números, conteo, aritmética, medición, visualización y análisis de datos básicos, y más.
A continuación, se muestran algunos de los temas clave en matemáticas primarias. Visite sus respectivas secciones para obtener información más detallada.
Números y conteo
Se puede pensar en los números como los componentes básicos de las matemáticas. Hay muchas clasificaciones y categorías de números diferentes, y comprender algunas de las claves es un aspecto importante del aprendizaje de muchos conceptos matemáticos.
El concepto de números se aprende comúnmente como parte del conteo, una de las primeras cosas que debemos aprender en matemáticas. Hay muchas formas diferentes de abordar la enseñanza o aprender a contar, y puede variar en todo el mundo. Contar objetos, como en la figura siguiente, es una de las muchas formas de abordar la enseñanza y el aprendizaje de contar.
En la práctica, los objetos físicos se pueden usar y mover para contar de uno en uno. El conteo es la base de la suma, que a su vez se acumula en otras operaciones aritméticas como la resta, la multiplicación y la división.
Aritmética
La aritmética básica involucra principalmente los conceptos de suma, resta, multiplicación y división. La exponenciación y las raíces también son parte de la aritmética, pero generalmente se aprenden más tarde que los otros temas aritméticos. La aritmética se utiliza en diversos grados en todas las áreas de las matemáticas.
Reglas y propiedades
Hay muchas reglas y propiedades de los números u otros objetos matemáticos que una persona necesita aprender para poder abordar con eficacia temas matemáticos como el álgebra, que se utiliza en todas las áreas de las matemáticas. La propiedad conmutativa, la propiedad distributiva y el orden de operaciones (PEMDAS o BODMAS) son solo algunos ejemplos.
Medición
La medición es la cuantificación de alguna propiedad de un objeto o evento que permite la comparación entre otros objetos o eventos. Es una parte fundamental de muchas áreas de las matemáticas, la ciencia, la tecnología y más. También es útil para simplemente interactuar con otras personas y el mundo que nos rodea. Entre los ejemplos cotidianos de medidas se incluyen la altura, el peso, la temperatura y la distancia.
Hay muchos sistemas de medición diferentes. El Sistema Internacional de Unidades (SI) es el sistema de medición más utilizado. Otros incluyen los sistemas de medición imperiales y consuetudinarios de EE. UU. Si bien muchos países de todo el mundo tienen sus propias unidades de medida locales, es importante que existan sistemas estandarizados como el SI a nivel mundial para que los países puedan comunicarse de manera efectiva. Por tanto, es importante aprender o reconocer varios sistemas de medida y poder convertir medidas entre sistemas.
Datos y gráficos
Los datos son unidades de información que a menudo se adquieren mediante observación y/o medición. Los gráficos son herramientas que se utilizan para representar datos de manera eficiente y más fácil de interpretar para las personas. A continuación se muestra un gráfico de líneas, uno de los muchos tipos diferentes de gráficos. Representa la estatura promedio de niños y niñas en centímetros de 0 a 20 años.
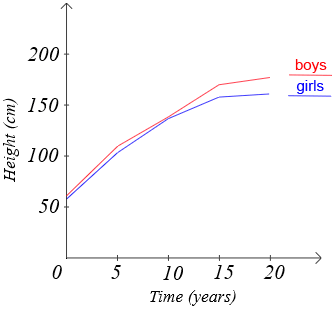
Podríamos haber escrito la edad promedio de cada año, o ponerla en una tabla, y habría transmitido los mismos datos. Sin embargo, ponerlo en un gráfico de líneas nos da una representación visual clara de los datos que rápidamente nos da una idea de las diversas relaciones entre las alturas de niños y niñas en relación con la edad. Sin el uso de gráficos, ciertos datos, aunque sean significativos, serían muy difíciles de interpretar.



