Un logaritmo es la función inversa de exponenciación . Un logaritmo nos dice la potencia , y, a la que se debe elevar una base, b, para que sea igual a x. Esto está escrito como:
log b (x)=y
Ejemplo
Escribe el equivalente a 10 3 =1000 usando logaritmos.
Dos de las bases más utilizadas son la base 10 (logaritmo común) y la base e (logaritmo natural). Generalmente, cuando alguien dice (o escribe) «log» sin especificar la base, la convención es asumir la base 10. Sin embargo, hay quienes se refieren al log natural (ln), como «log». Como tal, es importante saber en qué contexto se usa el término. Para evitar ambigüedad, es más seguro usar «log» para referirse a logaritmos de base 10 y «ln» o «log natural» para referirse a base e logaritmos. En otras palabras, «log (x)» normalmente indica log 10 (x) y ln (x) indica log e (x).
La intención de los logaritmos es ayudar a simplificar los cálculos en áreas como ciencia, ingeniería, física y matemáticas. La base 10 se usa más en ciencia e ingeniería, mientras que la base e se usa más en física y matemáticas. Los logaritmos también pueden involucrar decimales, no solo números enteros, pero calcularlos es más difícil e implica el uso de conceptos matemáticos más complicados, como las series de potencias. El uso de tablas de logaritmos precalculados también es relativamente común, aunque la llegada de las calculadoras electrónicas ha disminuido la necesidad de estas.
Función de logaritmo
A continuación se muestra una gráfica de f (x)=log (x) y f (x)=ln (x).
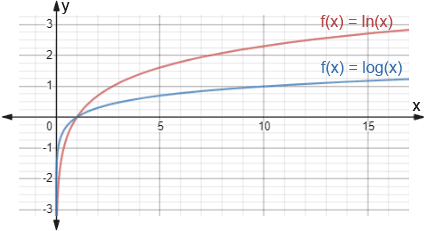
Como puede verse en el gráfico, una función logarítmica no puede tener un valor x negativo y tiene un cero en x=1 porque cualquier valor elevado a la th potencia 0 es igual a 1 (log b (1)=0). Cuando x se acerca a 0, una función logarítmica se acerca a -∞. Cuando x se acerca a ∞, la función se acerca a ∞. Además, cuanto menor es la magnitud de la base, más rápido aumenta la función logarítmica.
¿Por qué los logaritmos no pueden ser negativos?
Si bien el valor de un logaritmo puede ser un número negativo, el argumento (valor x) de cualquier logaritmo no puede ser negativo. Esto se debe a que la base de un logaritmo solo puede ser un número positivo mayor que 1, y un número positivo elevado a cualquier valor será un número positivo:
base & gt; 1
La base de un logaritmo no puede ser negativa porque una base negativa elevada a una fracción solo tiene una solución imaginaria. Una base de 0 siempre resultaría en 0, ya que 0 elevado a cualquier valor es 0, y una base de 1 siempre resultará en 1. Por lo tanto, la base de un logaritmo tiene que ser un número positivo distinto de 1, mayormente mayor que 1 .
Exponentes de números positivos
Dado que la base de un logaritmo debe ser positiva, sabemos que el argumento también debe ser positivo, ya que el argumento de un logaritmo es el resultado de elevar la base a algún número, e independientemente de cuál sea ese número, el resultado será sea positivo porque:
- Un número positivo elevado a un exponente positivo da como resultado un número positivo.
- Un número positivo elevado a la potencia 0 th es 1, un número positivo.
- Un número positivo elevado a una potencia negativa es solo el recíproco de ese número elevado a una potencia positiva.



