Cuando dos líneas se cruzan en un ángulo recto , th Son líneas perpendiculares. También podemos decir que si 2 rectas son perpendiculares, entonces su intersección forma un ángulo recto. A veces, en el lenguaje cotidiano, las partes de las líneas (rayos y segmentos de línea ) que se encuentran en ángulos rectos también se denominan líneas perpendiculares.
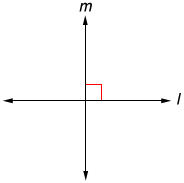
Las líneas lym son perpendiculares porque se encuentran en ángulo recto. Podemos escribir l⊥m para mostrar esto, donde «⊥» es el símbolo de perpendicular.
Además, si dos líneas son perpendiculares, se crean 4 ángulos rectos. En el siguiente diagrama, los ángulos 1, 2, 3, 4 son todos ángulos rectos.
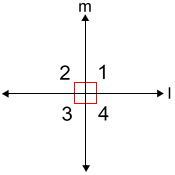
Propiedades de las líneas perpendiculares
• Solo puede haber una línea que sea perpendicular a una línea determinada en un punto determinado.
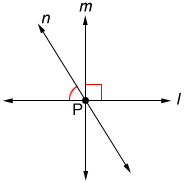
Deje que las líneas m, n y l se crucen en el punto P anterior. Si el ángulo formado por lym es un ángulo recto, entonces el ángulo formado por las líneas lyn no puede ser también un ángulo recto.
• Dos líneas son perpendiculares si sus pendientes son recíprocas negativas (o opuestas) entre sí.
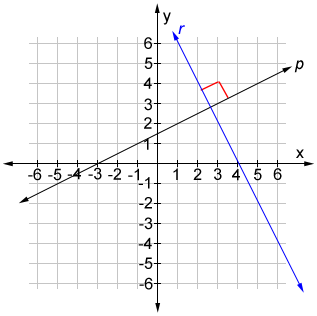
La pendiente de la recta p es ½ y la pendiente de la recta r es -2, el recíproco negativo de ½, por lo que pyq son perpendiculares y se encuentran en un ángulo recto.
Saber que dos líneas perpendiculares se encuentran en ángulo recto, o que si su intersección forma un ángulo recto, son perpendiculares, es información útil para trabajar con postulados, teoremas y otras propiedades en geometría. A continuación se muestran algunos ejemplos.
• Si los dos lados no adyacentes de dos ángulos adyacentes agudos son perpendiculares, los ángulos deben ser complementarios .

∠BAD y ∠CAD son ángulos adyacentes, con lados perpendiculares no adyacentes y . Dado que y son perpendiculares, ∠BAC es un ángulo recto que mide 90 °, por lo que ∠BAD + ∠CAD=90 ° .
• Si una transversal es perpendicular a una de un par de líneas paralelas (o varias líneas paralelas), debe ser perpendicular a todas las paralelas. líneas.
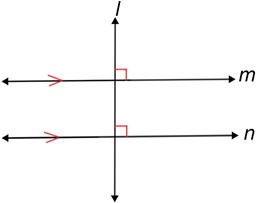
En el diagrama anterior, m // n y l⊥m. Dado que l⊥m, los cuatro ángulos formados por la intersección de l y m son ángulos rectos. Además, dado que m // n, los cuatro ángulos son también ángulos rectos formados por las líneas l y n, por la propiedad de que los ángulos correspondientes de las líneas paralelas son congruentes. Por lo tanto, la línea l también es perpendicular a la línea n.
¿Sabías que?
El x- y y-axis son dos líneas en el planos de coordenadas cartesianos que son perpendiculares entre sí.
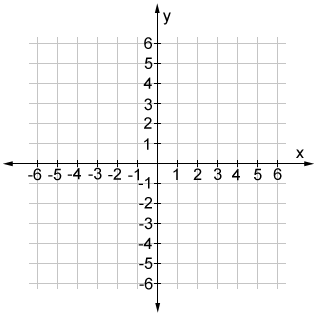
Además, cada línea de cuadrícula horizontal es perpendicular a cada línea de cuadrícula vertical que comprende la cuadrícula del sistema. El sistema de coordenadas cartesianas también se conoce como un sistema de coordenadas ortogonal (es decir, en ángulos rectos).



