Las funciones trigonométricas son funciones relacionadas con un ángulo . Hay seis funciones trigonométricas: seno, coseno, tangente y sus recíprocos cosecante, secante y cotangente, respectivamente. El seno, el coseno y la tangente son las funciones trigonométricas más utilizadas. Sus recíprocos, aunque se usan, son menos comunes en las matemáticas modernas. Las funciones trigonométricas también se denominan funciones circulares.
Hay dos formas principales en las que las funciones trigonométricas se suelen discutir: en términos de triángulos rectángulos y en términos de círculo de unidad . La definición de triángulo rectángulo de las funciones trigonométricas suele ser la forma en que se introducen, seguida de sus definiciones en términos del círculo unitario.
Definición de triángulo rectángulo
La salida de una función trigonométrica es una razón de las longitudes de dos lados de un triángulo rectángulo. Considere un ángulo θ como un ángulo en un triángulo rectángulo. Las siguientes son las definiciones de las funciones trigonométricas. Estas funciones a menudo se escriben en sus formas abreviadas.
| seno: | |
| coseno: | |
| tangente: |
| cosecante: | |
| secante: | |
| cotangente: |
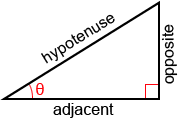
Los términos que se utilizan para describir los lados de un triángulo rectángulo son hipotenusa, el lado adyacente y el lado opuesto, como se muestra en la figura anterior.
- Adyacente: el lado junto a θ que no es la hipotenusa
- Opuesto: el lado opuesto θ.
- Hipotenusa: el lado más largo del triángulo opuesto al ángulo recto.
Un método común para recordar las relaciones anteriores es mediante el uso del mnemónico «soh cah toa». La s, c y t representan seno, coseno y tangente, y o, a y h representan opuesto, adyacente e hipotenusa.
Cosecante, secante y cotangente son los recíprocos de seno, coseno y tangente, respectivamente. Como tal, siempre que recordemos las definiciones de seno, coseno y tangente, podemos tomar sus recíprocos para determinar las definiciones de cosecante, secante y cotangente.
Ejemplo:
Encuentre los valores de los seis trigonométricos dado el siguiente triángulo rectángulo.
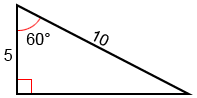
La hipotenusa del triángulo es 10 y el lado adyacente tiene una longitud de 5. Utilizando el teorema de Pitágoras , podemos encontrar la longitud del tercero, opuesto, lado:
5 2 + b 2 =10 2
25 + b 2 =100
b 2 =75
Ahora que conocemos todos los lados del triángulo con referencia al ángulo, 60 °, podemos conectarlos a las funciones trigonométricas como se definió anteriormente:
Definición de círculo unitario
Las funciones trigonométricas también se pueden definir como valores de coordenadas en un círculo unitario. Un círculo unitario es un círculo de radio 1 centrado en el origen. La definición de triángulo rectángulo de funciones trigonométricas permite ángulos entre 0 ° y 90 ° (0 y en radianes). El uso de las definiciones de círculos unitarios nos permite extender el dominio de las funciones trigonométricas a todos los números reales. Consulte la figura siguiente.
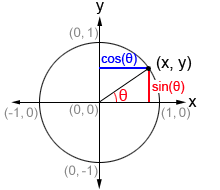
Dado un punto (x, y) en el círculo unitario, podemos formar un triángulo rectángulo, como se muestra en la figura. En tal triángulo, la hipotenusa es el radio del círculo unitario, o 1. θ es el ángulo formado entre el lado inicial de un ángulo a lo largo del eje x y el lado terminal del ángulo formado al girar el rayo en el sentido de las agujas del reloj o en sentido anti-horario. El lado terminal del ángulo es la hipotenusa del triángulo rectángulo y es el radio del círculo unitario. Por lo tanto, siempre tiene una longitud de 1. El punto en el que el lado terminal del ángulo interseca el círculo unitario tiene un valor x de cos (θ) y un valor y de sin (θ).
Por lo tanto, en el círculo unitario, el coseno y el seno se pueden definir como:
Para tan (θ), x no puede ser igual a 0.
Cosecante, secante y cotangente son los recíprocos de seno, coseno y tangente respectivamente, y se definen como:
Los valores de las funciones trigonométricas también se pueden representar mediante las longitudes de los segmentos de línea en un plano de coordenadas con un círculo unitario, como se muestra en el diagrama a continuación.
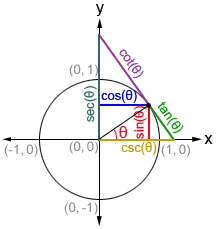
Valores de la función trigonométrica para los ángulos especiales
Los valores de las funciones trigonométricas se pueden encontrar a través de los valores de las coordenadas de las intersecciones en un círculo unitario. Si bien podemos encontrar el valor de cualquiera de las funciones trigonométricas para cualquier valor de θ, existen algunos ángulos que se usan con más frecuencia en trigonometría y que vale la pena memorizar. La siguiente es una lista de los valores de las funciones seno, coseno y tangente de ángulos especiales en el primer cuadrante .

Ángulo de referencia
Los ángulos agudos en el primer cuadrante se pueden usar para determinar los valores de las funciones trigonométricas de los ángulos en otros cuadrantes. Estos ángulos se denominan ángulos de referencia ya que haremos referencia a sus valores para determinar otros valores. Siempre es el ángulo más pequeño (con referencia al eje x) que se puede formar desde el lado terminal de un ángulo. Las figuras siguientes muestran un ángulo θ y su ángulo de referencia θ ‘en un cuadrante diferente al primer cuadrante.
| Cuadrante II | Cuadrante III | Cuadrante IV |
|---|---|---|
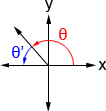 | 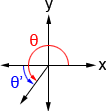 | 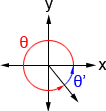 |
| θ ‘= 180 ° – θ | θ ‘= θ – 180 ° | θ ‘= 360 ° – θ |
Si un ángulo es un ángulo de referencia de otro, las funciones trigonométricas de estos dos ángulos tienen los mismos valores en magnitud, y solo debemos prestar atención a sus signos basados en el cuadrante en el que se encuentra el lado terminal del ángulo. . Por ejemplo, 30 ° es el ángulo de referencia de 210 ° con valores de seno sin (30 °)=y sin (210 °)=
. Podemos ver que los valores de seno de ambos tienen una magnitud de
, aunque tienen diferentes signos.
A continuación se muestra una tabla que muestra los signos de las 6 funciones trigonométricas en cada cuadrante.
| Sin | Cos | Tan | Csc | Sec | Cuna | |
| Cuadrante I | + | + | + | + | + | |
| Cuadrante II | + | – | – | + | – | |
| Cuadrante III | – | – | + | – | + | |
| Cuadrante IV | – | + | – | – | – |
Una vez que determinamos el ángulo de referencia, podemos determinar el valor de las funciones trigonométricas en cualquiera de los otros cuadrantes aplicando el signo apropiado a su valor para el ángulo de referencia.
Ejemplo:
Utilice ángulos de referencia para encontrar los valores de cos (150 °) y sin (315 °).
Dado que 150 ° está en el cuadrante II, el ángulo de referencia para 150 ° es, 180 ° -150 °=30 ° donde, cos (30 °)=. Además, debido a que 150 ° está en el cuadrante II, el coseno es negativo entonces, cos (150 °)=
.
Dado que 315 ° está en el cuadrante IV, el ángulo de referencia para 315 ° es, 360 ° -315 °=45 ° donde, sin (45) °=. Además, debido a que 315 ° está en el cuadrante IV, el seno es negativo, sin (315 °)=
.
Las funciones trigonométricas son funciones periódicas
Una función periódica es una función, f, en la que existe algún valor positivo, p, tal que
f (x + p)=f (x)
para todo x en el dominio de f, p es el número positivo más pequeño para el cual f es periódico, y se conoce como el período de f.
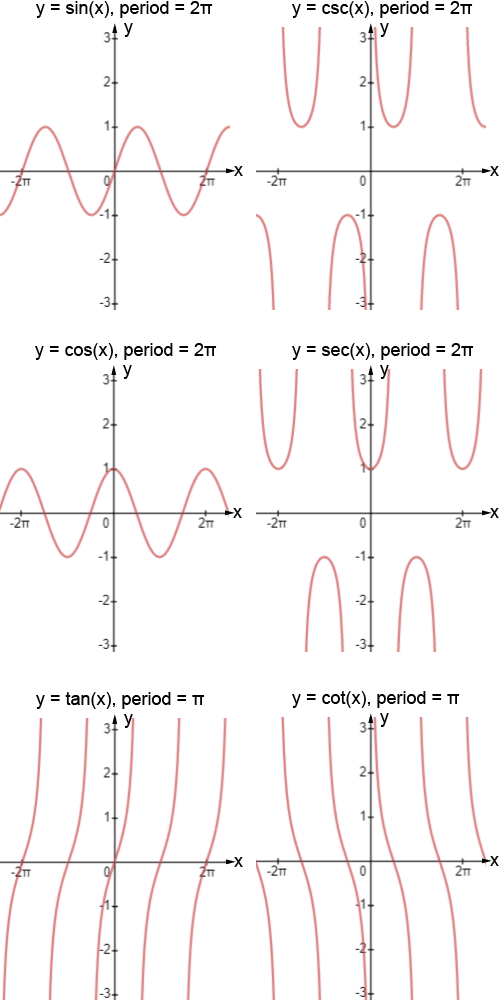
Las 6 funciones trigonométricas son funciones periódicas. No importa en qué punto empecemos en el círculo unitario, si viajamos una distancia de 2π (360 °) a lo largo del círculo unitario desde ese punto, llegaremos a nuestro punto de partida, lo que indica que la función trigonométrica tiene el mismo valor. en el ángulo. Esto significa que las funciones trigonométricas repiten sus valores.
Las funciones seno, coseno, cosecante y secante tienen un período de 2π. Las funciones tangente y cotangente tienen un período de π.
sin (θ + 2π)=sin (θ)
cos (θ + 2π)=cos (θ)
csc (θ + 2π)=csc (θ)
seg (θ + 2π)=seg (θ)
tan (θ + π)=tan (θ)
cuna (θ + π)=cuna (θ)
Ejemplo:
Busque cos () y tan (
) usando sus puntos.
Las funciones trigonométricas son pares o impares
Una función impar es una función en la que -f (x)=f (-x). Tiene simetría sobre el origen. Una función par es una función en la que f (x)=f (-x), lo que significa que al reflejar el gráfico en el eje y se obtendrá el mismo gráfico. De las 6 funciones trigonométricas, seno, tangente, cosecante y cotangente son funciones impares. El coseno y la secante son funciones pares. Por lo tanto:
| Funciones pares | Funciones impares |
|---|---|
| cos (-θ)=cos (θ) sec (-θ)=sec (θ) | sin (-θ)=-sin (θ) tan (-θ)=-tan (θ) csc (-θ)=-csc (θ) cot (-θ)=-cot (θ) |
Funciones trigonométricas inversas
Las funciones trigonométricas inversas son las funciones inversas de las funciones trigonométricas. Específicamente, son arcoseno, arcocoseno, arcotangente, arcososecante, arcosecante y arcangente. La entrada de las funciones trigonométricas inversas son las relaciones trigonométricas de un ángulo y su salida es el ángulo:
θ=arcsin (x), donde –1≤x≤1 θ=arccos (x), donde –1≤x≤1 θ=arctan (x) θ=arccsc (x), donde x≤-1 o 1≤x θ=arcsec (x), donde x≤-1 o 1≤x θ=arctan (x) |
Las funciones trigonométricas inversas también se escriben como sin -1 (x), cos -1 (x), tan -1 (x), csc -1 (x), sec -1 (x) y cot -1 (x ).
Ejemplo:
Dado sin (30 °)=0.5, ¿qué es arcsin (0.5)?
arcsin (0.5)=30 °
Nota: esto solo proporciona el resultado en el primer cuadrante. Si considera otros cuadrantes, arcsin (0.5) también es igual a 150 °. Además, dado que arcsin es una función periódica, para dar cuenta de todos los valores posibles de arcseno, debemos tener en cuenta su periodicidad. Por tanto, la solución es
30 ° + n × 360 ° o 150 ° + n × 360 °
donde n es un número entero. Cuando se utilizan las otras funciones trigonométricas inversas, su periodicidad también debe tenerse en cuenta para determinar todas las soluciones.
Gráficos de las funciones trigonométricas
La siguiente figura muestra los gráficos de varios períodos de las seis funciones trigonométricas. Consulte las páginas seno , coseno y tangente para una explicación detallada sobre cómo graficar funciones trigonométricas que han sufrido ciertas transformaciones (las mismas explicaciones se aplican a cosecante, secante y cotangente, con pequeñas diferencias).