Una función es una relación entre dos conjuntos en la que cada miembro del primer conjunto está emparejado con uno, y solo uno, miembro del segundo conjunto.
Una regla de función es una regla que explica la relación entre dos conjuntos.
Ejemplo
Dos de las formas en que se pueden mostrar las funciones son mediante el uso de mapas (izquierda) y tablas (derecha), que se muestran a continuación.
 | 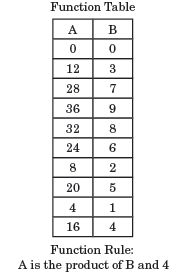 |
Las funciones también se representan algebraicamente mediante expresiones o ecuaciones. Estas expresiones y ecuaciones describen la relación entre una variable independiente y una dependiente.
Ejemplo
3x + 4 f (x)=x
Las funciones también se pueden dibujar como gráficos. Cuando se representa como gráficos, la variable dependiente de la función se traza en el eje y, mientras que la variable independiente se traza en el eje x. Para funciones discretas, cada punto de la función (x, y) se traza como una coordenada. Para funciones no discretas, esos puntos están conectados como una línea.
Ejemplo
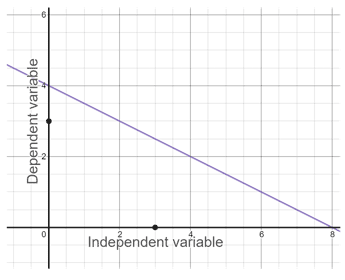
En un gráfico, la prueba de la línea vertical se puede utilizar para determinar si una curva es una función o no. También existe la prueba de la línea horizontal, que determina si una función es uno a uno. Una función uno a uno se define como una función en la que los elementos distintos de su dominio nunca se asignan al mismo elemento de su co-dominio, como se muestra a continuación:
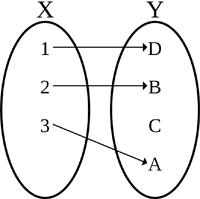 | 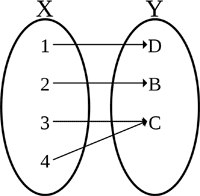 |
A la izquierda hay una función uno a uno, también conocida como función inyectiva. Ningún elemento X se asigna al mismo elemento Y. Por el contrario, la función de la derecha es una función que no es uno a uno, ya que dos de los elementos X, 3 y 4, están asignados al mismo elemento Y, C.



