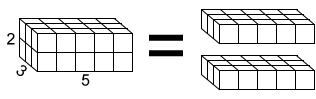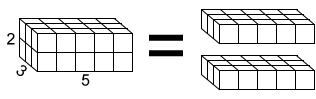El volumen de un forma 3D o figura geométrica es la cantidad de espacio que contiene. El volumen está bien definido para muchas formas comunes; las fórmulas para algunas formas comunes se muestran a continuación.
Cubo
El volumen, V, de un cubo con borde, s, es:
V=s 3

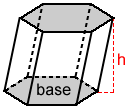
Prisma
El volumen, V, de un prisma es:
V=Bh
donde B es el área de la base y h es la altura del prisma.
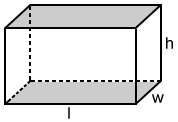
Prisma rectangular
El volumen, V, de un prisma rectangular es:
V=lwh
donde l es la longitud, w es el ancho y h es la altura del prisma rectangular.
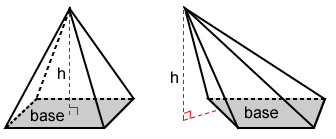
Pirámide
El volumen, V, de una pirámide es:
donde B es el área de la base y h es la altura de la pirámide.
Cono
El volumen, V, de un cono es:
donde r es el radio de la base y h es la altura del cono.
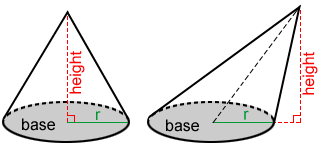
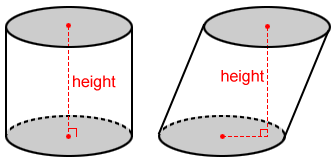
Cilindro
El volumen, V, de un cilindro es:
V=πr 2 h
donde r es el radio de la base y h es la altura del cilindro.
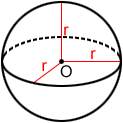
Esfera
El volumen, V, de una esfera con radio, r, es:
Ejemplo:
Encuentre el volumen del prisma rectangular a continuación.
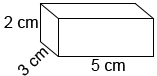
El volumen del prisma rectangular es:
V=5 × 3 × 2=30 cm 3
Volumen de una figura compuesta
Las figuras compuestas en 3D son figuras que se componen de dos o más tipos de figuras. Sus volúmenes se pueden calcular dividiéndolos en sus componentes, calculando los volúmenes de cada componente y luego sumándolos para encontrar el volumen total de la figura compuesta.
Ejemplo:
El silo de granos de abajo está formado por un cilindro recto y un cono circular recto. Calcula la cantidad de grano, en metros cúbicos, que el silo puede contener cuando está lleno.
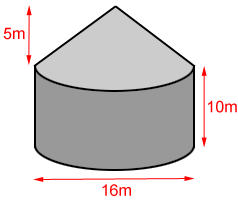
El cilindro tiene un radio de 8 my una altura de 10 m. El cono también tiene un radio de 8 m, ya que se asienta sobre el cilindro, y su altura es de 5 m.
El volumen del cilindro es:
V cilindro =π × 8 2 × 10=640π m 3
El volumen del cono es:
El silo tiene capacidad para 2345,72 metros cúbicos de grano.
Usar un cubo unitario para encontrar el volumen
Una forma de encontrar el volumen de una figura es determinar cuántas unidades de cubos se necesitan para llenar la figura. Un cubo unitario tiene lados de 1 y un volumen de 1.
El prisma rectangular de abajo tiene una longitud de 5, un ancho de 3 y una altura de 2.
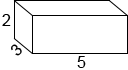

Puede apilar uniformemente 2 capas de cubos unitarios, que contienen un total de 15 cubos unitarios cada uno, en el prisma rectangular para encontrar su volumen de cubos 30 unitarios.