Una ecuación lineal es una ecuación que representa una línea recta. Cuando se traza en un gráfico, una ecuación lineal siempre da como resultado una línea recta, como en la figura siguiente, que es un caso especial de una ecuación lineal denominada función identidad, y=x:
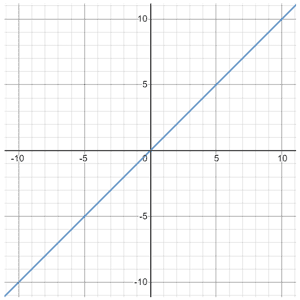
Se la conoce como función de identidad porque ingresar cualquier valor x devolverá el mismo valor de y.
En la mayoría de los casos, el término «ecuación lineal» se refiere a ecuaciones lineales de una variable (como la anterior), aunque las ecuaciones lineales pueden tener más variables, siempre que todas las variables sean de primer orden. Una variable de primer orden, también conocida como variable de grado 1, se refiere al exponente de la variable. Por ejemplo, la siguiente ecuación no es una ecuación lineal. El grado de cada término se incluye como referencia, aunque por convención, generalmente solo se muestran los exponentes que no son 0 o 1:
y 1 =2x 3 – 3x 1 + 4 0
El grado de un polinomio está determinado por el término de mayor orden en el polinomio. En esta ecuación, el grado más alto es 3, lo que hace que la ecuación no sea lineal. Todas las variables involucradas deben ser de grado 1 para que la ecuación sea lineal.
Puede estar presente cualquier número de constantes (ya que su grado es 0). Si una ecuación solo tiene una constante, la ecuación es una línea horizontal (ej. Y=4) o vertical (ej. X=-2).
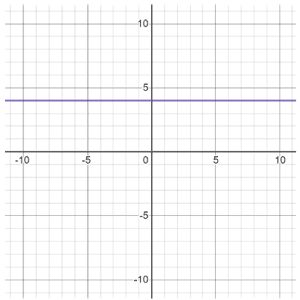 y=4 | 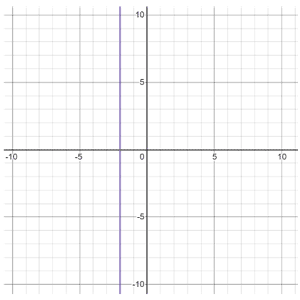 x=-2 |
Formas de ecuaciones lineales
Las ecuaciones lineales pueden adoptar varias formas, incluidas forma pendiente-intersección, forma punto-pendiente, formulario estándar y más.
Forma pendiente-intersección
La forma pendiente-intersección es probablemente la forma más utilizada de una ecuación lineal. Normalmente se expresa como
y=mx + b
donde m es la pendiente y b es la intersección con el eje y.
La ecuación de una línea se puede escribir en forma pendiente-intersección cuando se conocen la pendiente y la intersección y de la línea. O, dada una ecuación en forma pendiente-intersección, es fácil identificar rápidamente la pendiente y la intersección y de la línea. Graficar la ecuación de una línea también es relativamente simple cuando se le da una ecuación en forma pendiente-intersección.
Forma punto-pendiente
La forma punto-pendiente es similar a la forma pendiente-intersección, excepto que se basa en algún punto de la línea, en lugar de la intersección en y específicamente. Normalmente se expresa como
y – y 1 =m (x – x 1 )
donde (x 1 , y 1 ) representan un punto en la línea y m es la pendiente. Al igual que la forma pendiente-intersección, también es útil para graficar y tiene la ventaja de ser utilizable usando cualquier punto de la línea en lugar de solo la intersección con el eje y específicamente, como es el caso con la forma pendiente-intersección.
Forma estándar
La forma estándar para la ecuación de una línea se expresa típicamente como
Ax + By=C
Donde A, B y C son números enteros, y A y B no son iguales a 0. Uno de los beneficios clave de la forma estándar sobre la forma pendiente-intersección o punto-pendiente es que se puede utilizar para encontrar rápidamente la X-intersección. También se puede usar para encontrar la intersección con el eje y de una línea, pero esto es algo que también es relativamente fácil al usar cualquiera de las otras formas. Una vez que se conocen la intersección con el eje x y la intersección con el eje y, también se puede usar la forma estándar para graficar la línea, aunque es un poco más tedioso que usar cualquiera de las otras dos formas mencionadas.
La forma estándar también es la forma de una ecuación lineal que se usa típicamente al resolver sistemas de ecuaciones lineales. El uso de la forma pendiente-intersección o punto-pendiente dificultaría la resolución de ecuaciones lineales.
Las ecuaciones lineales también se expresan en otras formas, pero las anteriores son algunas de las más comunes.



