El conjunto de todos los puntos en un plano que son equidistantes de un fijo El punto, definido como el centro, se llama círculo.
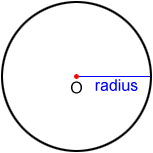
El círculo de arriba se llama círculo O. Un segmento de línea con dos extremos , uno en el centro y el otro en el perímetro del círculo, forma un radio, r, del círculo.
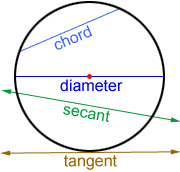
Una cuerda es un segmento de línea cuyos extremos se encuentran en el perímetro del círculo. Si la cuerda contiene el centro, se llama diámetro del círculo. El diámetro es el doble de la longitud del radio.
Una línea se llama línea secante si se cruza con el círculo en dos puntos. Una línea se llama línea tangente si interseca al círculo en un solo punto, llamado punto de tangencia.
Los círculos se estudian ampliamente en geometría. Los siguientes son algunos conceptos importantes relacionados con los círculos.
Circunferencia
La circunferencia, C, de un círculo es similar al perímetro de un polígono en que es una medida de la distancia alrededor del círculo.
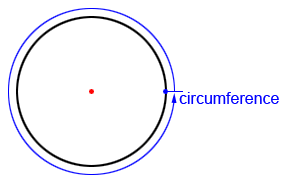
La circunferencia del círculo anterior se puede encontrar usando la fórmula
C=2πr
donde r es el radio del círculo. También puede usar la fórmula C=πd , donde d es el diámetro del círculo. π es una constante matemática que representa la relación entre la circunferencia del círculo y su diámetro. Es aproximadamente igual a 3,14.
Ejemplo:
La siguiente figura muestra el círculo A con radio AB=4.4 que tiene una circunferencia
C=2π · 4.4=27.6.
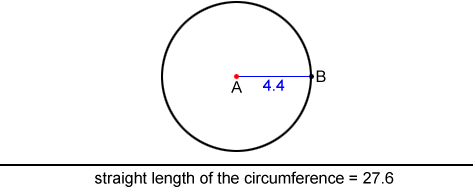
El segmento de línea debajo del círculo representa la longitud recta de su circunferencia.
Arco de un círculo
Un arco de un círculo es parte de un círculo.
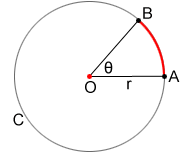
Arc AB, escrito simbólicamente como , se muestra en rojo para el círculo O.
se llama arco menor ya que abarca menos de la mitad de la circunferencia de los círculos.
se denomina arco mayor ya que abarca más de la mitad de la circunferencia del círculo. Los arcos menores generalmente se nombran usando dos puntos, mientras que los arcos mayores generalmente se nombran usando tres.
La longitud de un arco es una parte de la longitud de la circunferencia de un círculo. Se puede calcular mediante la fórmula,
donde θ es el ángulo central, en unidades de grados, subtendido por el arco. Si el ángulo se da en radianes, la longitud del arco se puede encontrar usando:
s=rθ
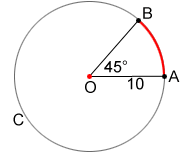
Para el círculo O a continuación, la medida de es
Área
El área de un círculo es la región plana delimitada por la circunferencia del círculo. El área se mide en unidades cuadradas de longitud, mientras que la circunferencia se mide en unidades de longitud.
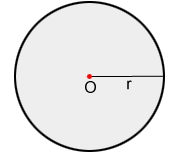
La región sombreada en gris dentro del círculo O arriba es su área. La fórmula para el área es
A=πr 2
donde r es el radio del círculo.
Sector
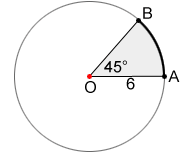
Un sector de un círculo es la región delimitada por dos radios y el arco que forman. El sector OAB a continuación, formado por radios OA, OB y , es la región gris del círculo O.
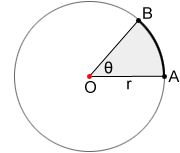
El área, A, de un sector se puede calcular mediante la fórmula,
donde θ es el ángulo central (en grados) que forma el sector. Si el ángulo se da en radianes, el área del sector se puede encontrar usando:
Para el círculo O a continuación, el área del sector OAB es
Alternativamente, el área de un sector se puede encontrar usando la fórmula,
donde r es el radio y s es la longitud del arco del sector.
¿Sabías que?
La región entre dos círculos concéntricos se denomina anillo. El nombre proviene de una raíz latina que significa «anillo pequeño». El término «anillo» también se usa para nombrar estructuras en forma de anillo, como el anillo de crecimiento anual de un árbol:




