El área de un triángulo es la región delimitada por sus tres lados.
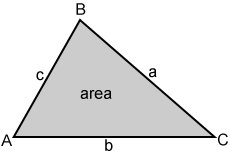
El área de un triángulo se puede encontrar usando varios métodos diferentes.
Uso de la base y la altura
Dadas la base by la altura h de un triángulo, el área del triángulo es:
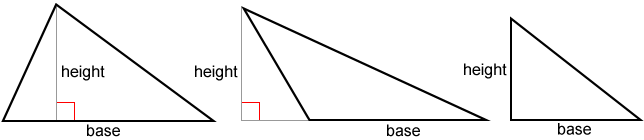
La altura de un triángulo es perpendicular a su base. Puede ser interior, exterior o lateral como se muestra en la siguiente figura.
La fórmula anterior se puede probar usando el área de un paralelogramo . La fórmula para el área de un paralelogramo es base × altura, escrita como Área=b × h. La diagonal de un paralelogramo lo divide en dos triángulos congruentes como se muestra en el paralelogramo ABCD a continuación.
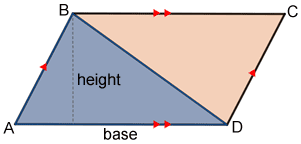
Dado que △ ABC≅ △ CBD, el área de △ ABC es la mitad del área del paralelogramo. Por lo tanto, el área de △ ABC=. Del mismo modo, el área de △ CBD=
.
Usando sus lados
Si se dan los tres lados de un triángulo, el área se puede encontrar usando la fórmula de Heron.
donde a, byc son las longitudes de los tres lados del triángulo, el semiperímetro, s, es .
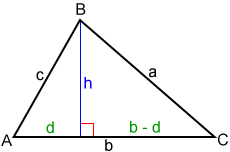
Una forma de probar la fórmula de Heron es usando el Teorema de Pitágoras . En la figura anterior, tenemos d 2 + h 2 =c 2 y (b – d) 2 + h 2 =a 2 . Restando estos obtenemos 2bd=b 2 + c 2 – a 2 . Entonces,
Desde h 2 =c 2 – d 2
| h 2 = | |
| = | |
| = | |
| = | |
| = | |
| = |
| Area= | |
| = | |
| = |
Uso de trigonometría
Si se dan dos lados y un ángulo incluido para un triángulo, podemos encontrar su área usando las siguientes fórmulas:
donde A, B y C son los 3 ángulos del triángulo y a, byc son las longitudes de los 3 lados opuestos a los 3 ángulos.
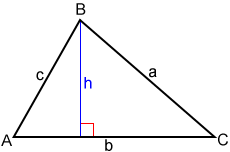
Para el triángulo que se muestra arriba con base b, altura h, lados a y ángulo C dados, podemos usar la función seno para obtener y encuentre que h=a × sin (C).
Usando Area=.



