El área de un trapezoide es el espacio contenido dentro de su perímetro . El espacio gris es el área del trapezoide en el siguiente diagrama.
Fórmula del área de un trapezoide
El área, A, de un trapezoide es:
donde h es la altura y b 1 yb 2 son las longitudes base.
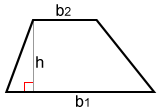
Derivación
Dado un trapezoide, si formamos un trapezoide congruente y lo rotamos de manera que los dos trapezoides congruentes se puedan unir para formar un paralelogramo como lo muestran los trapezoides negros y grises congruentes a continuación.
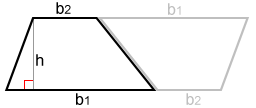
El área de un paralelogramo es A=bh. El paralelogramo formado por los dos trapezoides congruentes tiene una base b 1 + b 2 y una altura h. Por lo tanto, el área de este paralelogramo es:
A=(b 1 + b 2 ) h. Dado que el paralelogramo está formado por dos trapezoides congruentes, dividir a la mitad la fórmula anterior nos da la fórmula para el área de uno de los trapezoides:
Ejemplo:
Calcula el área de un trapezoide que tiene una altura de 16 y bases de 18 y 35.
Conectando estos en la fórmula del área:
Uso del segmento medio
El segmento medio de un trapezoide es un segmento de línea que conecta el punto medio de sus patas. Un segmento medio tiene una longitud que es el promedio de sus dos bases, que es
El área, A, de un trapezoide usando la longitud del segmento medio es:
A=hm
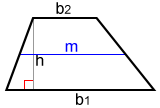
Derivación
Sustituyendo el valor de m en la fórmula del área trapezoidal original:
Encontrar área usando una cuadrícula
Otra forma de encontrar el área de un trapezoide es determinar cuántas unidades cuadradas se necesitan para cubrir su superficie. A continuación se muestra un cuadrado unitario con longitudes laterales de 1 cm.

Se puede usar una cuadrícula de cuadrados unitarios para determinar el área de un trapezoide.
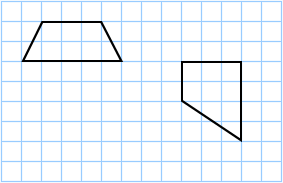
La cuadrícula de arriba contiene cuadrados unitarios que tienen un área de 1 cm 2 cada uno. El trapezoide de la izquierda contiene 6 cuadrados completos y 4 cuadrados parciales, por lo que tiene un área de aproximadamente:
El trapezoide de la derecha contiene 7 cuadrados completos y 4 cuadrados parciales, por lo que tiene un área de aproximadamente:
Este método se puede utilizar para encontrar el área de cualquier forma; no se limita a trapezoides. Sin embargo, es solo un valor aproximado del área. Cuanto más pequeña sea la unidad cuadrada utilizada, mayor será la precisión de la aproximación. Usar una cuadrícula formada por cuadrados de 1 mm es 10 veces más preciso que usar una cuadrícula formada por cuadrados de 1 cm.



