Arccosine, escrito como arccos o cos-1 (no confundir con ), es la función coseno inversa. El coseno solo tiene una inversa en un dominio restringido, 0≤x≤π. En la siguiente figura, la parte del gráfico resaltada en rojo muestra la parte del gráfico de cos (x) que tiene una inversa.
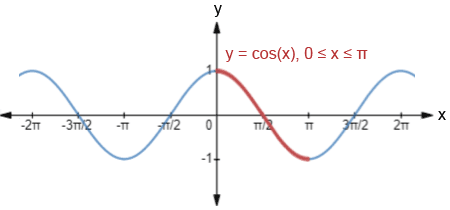
El dominio debe estar restringido porque para que una función tenga una inversa, la función debe ser uno a uno, lo que significa que ninguna línea horizontal puede intersecar la gráfica de la función más de una vez. Dado que el coseno es una función periódica, sin restringir el dominio, una línea horizontal intersecaría la función periódicamente, infinitas veces.
Una de las propiedades de las funciones inversas es que si un punto (a, b) está en la gráfica de f, el punto (b, a) está en la gráfica de su inversa. Esto significa efectivamente que la gráfica de la función inversa es un reflejo de la gráfica de la función a través de la línea y=x.
La gráfica de y=arccos (x) se muestra a continuación.
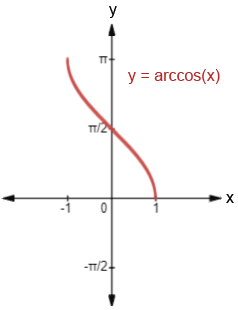
Como puede verse en la figura, y=arccos (x) es un reflejo de cos (x), dado el dominio restringido 0≤x≤π, a través de la línea y=x. El dominio de arccos (x), -1≤x≤1, es el rango de cos (x), y su rango, 0≤x≤π, es el dominio de cos (x).
Calculadora Arccos
La siguiente es una calculadora para averiguar el valor del arco de un número entre -1 y 1 o el valor del coseno de un ángulo.
| arccos | = | |||
Usar ángulos especiales para encontrar arcos
Si bien podemos encontrar el valor de arcocoseno para cualquier valor de x en el intervalo [-1, 1], existen ciertos ángulos que se usan con frecuencia en trigonometría (0 °, 30 °, 45 °, 60 °, 90 ° , y sus múltiplos y equivalentes en radianes) cuyos valores de coseno y arcocoseno puede valer la pena memorizar. A continuación se muestra una tabla que muestra estos ángulos (θ) en grados, y sus respectivos valores de coseno, cos (θ).
| θ | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 120 ° | 135 ° | 150 ° | 180 ° |
| cos (θ) | 1 | 0 | -1 |
Un método que puede ayudar a memorizar estos valores es expresar todos los valores de cos (θ) como fracciones que involucran una raíz cuadrada. Comenzando desde 0 ° y progresando a través de 90 °, cos (0 °)=1=. Los valores subsiguientes, cos (30 °), cos (45 °), cos (60 °) y cos (90 °) siguen un patrón tal que usando el valor de cos (0 °) como referencia, para encontrar los valores del coseno para los ángulos subsiguientes, simplemente disminuimos en 1 el número debajo del signo del radical en el numerador, como se muestra a continuación:
| θ | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| cos (θ) | 0 |
De 90 ° a 180 °, aumentamos el número debajo del radical en 1, pero también debemos tener en cuenta el cuadrante en el que está el ángulo. El coseno es negativo en los cuadrantes II y III, por lo que los valores serán iguales pero negativo. En los cuadrantes I y IV, los valores serán positivos. Este patrón se repite periódicamente para las respectivas medidas de ángulos.
Una vez que hemos memorizado los valores, o si tenemos una referencia de algún tipo, resulta relativamente sencillo reconocer y determinar los valores de coseno o arcocoseno para los ángulos especiales.
Ejemplo:
Busque arccos (), arccos (
) y arccos (2) en radianes.
,
.
,
.
arccos (2) no está definido porque 2 no está dentro del intervalo -1≤arccos (θ) ≤1, el dominio de arccos (x).
Propiedades inversas
Generalmente, las funciones y sus inversas exhiben la relación
f (f -1 (x))=x ; y ; f -1 (f (x))=x
dado que x está en el dominio de la función. Lo mismo ocurre con cos (x) y arccos (x) dentro de sus respectivos dominios restringidos:
cos (arccos (x))=x, para todo x en [-1, 1]
y
arccos (cos (x))=x, para todo x en [0, π]
Estas propiedades nos permiten evaluar la composición de funciones trigonométricas.
Composición de arcocoseno y coseno
Si x está dentro del dominio, evaluar una composición de arcocoseno y coseno es relativamente simple.
Ejemplos:
1.
2.
Si x no está dentro del dominio, necesitamos determinar el ángulo de referencia así como el cuadrante relevante. Dado arccos (cos ()), no podemos evaluar esto como lo hicimos anteriormente porque x no está dentro [0, π], por lo que la solución no puede ser
. Para evaluar esto, primero debemos determinar cos (
) antes de usar arccos:
3. »
En el ejemplo anterior, el ángulo de referencia es y cos (
) es
, pero como
se encuentra en el cuadrante III, su coseno es negativo y el único ángulo cuyo coseno es
, que se encuentra dentro del dominio de arccos (x), es
.
Composición de otras funciones trigonométricas
También podemos hacer composiciones usando todas las demás funciones trigonométricas: seno, tangente, cosecante, secante y cotangente.
Ejemplo:
Encuentra sin (arccos ()).
Dado que no es una de las proporciones para los ángulos especiales, podemos usar un derecho triángulo para encontrar el valor de esta composición. Dado arccos (
)=θ, podemos encontrar que cos (θ)=
. El siguiente triángulo rectángulo muestra θ y la razón de su lado adyacente a la hipotenusa del triángulo.
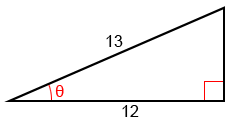
Para encontrar el seno, necesitamos encontrar el lado opuesto ya que sin (θ)=. Sea a la longitud del lado opuesto. Usando el teorema de Pitágoras,
a 2 + 12 2 =13 2
a 2 + 144=169
a 2 =25
a=5
y
sin (arccos ())=sin (θ)=
El mismo proceso se puede utilizar con una expresión variable.
Ejemplo:
Busque tan (arccos (4x)).
Dado arccos (4x)=θ, podemos encontrar que cos (θ)=y construir el siguiente triángulo rectángulo:

Para encontrar la tangente, necesitamos encontrar el lado opuesto, ya que tan (θ)=. Sea b la longitud del lado opuesto. Usando el teorema de Pitágoras,
(4x) 2 + b 2 =1 2
16x 2 + b 2 =1
b 2 =1 – 16x 2
b=
y
tan (arccos (4x))=tan (θ)=, donde –
& lt; x & lt;
Uso del arcocoseno para resolver ecuaciones trigonométricas
Arccosine también se puede usar para resolver ecuaciones trigonométricas que involucran la función coseno.
Ejemplo:
Resuelve las siguientes ecuaciones trigonométricas para x donde 0≤x & lt; 2π.
1. 2cos (x)=
2cos (x)=
cos (x)=
x=arccos ()
El coseno es negativo en los cuadrantes II y III, por lo que hay dos soluciones: x=y x=
. Estos son los únicos dos ángulos dentro de 0≤x & lt; 2π cuyo valor de coseno es igual a
.
2. 6cos 2 (x) + 9cos (x) – 36=0
6cos 2 (x) + 9sin (x) – 6=0
(6cos (x) – 3) (cos (x) + 2)=0
6cos (x) – 3=0 o cos (x) + 2=0
cos (x)=o cos (x)=-2
x=arccos () o x=arccos (-2)
Resolviendo para x=arccos (),
x=o
No podemos resolver x=arccos (-2) porque no está definido, por lo que x=o
son las únicas soluciones.



