El algoritmo de Euclides es un método para calcular el máximo común divisor (MCD). No solo funciona para los números naturales, sino para cualquier conjunto en el que exista una «división con residuo». A este tipo de divisiones en la que existe residuo se les nombra divisiones euclidianas y a los conjuntos donde se puede definir dicha división se les llama dominios euclídeos.
En resumen, podemos decir que el algoritmo de Euclides extendido es una ligera modificación del algoritmo de Euclides, y también nos permite expresar el máximo común divisor como una combinación lineal. El algoritmo tiene aplicaciones en varios campos, como álgebra, teoría de números e informática.
Qué es el máximo común divisor (MCD)
En matemáticas, denominamos máximo común divisor o MCD al mayor número que divide exactamente a dos o más números a la vez. Como hablamos del mayor número solo tendremos en cuenta los divisores positivos. Podemos decir que en “A” y “B”, es el número mayor que los divide a los dos, tanto al número A como al número B.
En un ejemplo sobre el máximo común divisor de 18 y 24 es 6, porque 6 es el mayor de los divisores comunes de 18 y 24 y lo escribimos MCD (18,24) = 6
Calculamos el máximo común divisor con un ejemplo
Vamos a utilizar 2 métodos:
- Método 1; buscando los divisores de un número
- Método 2; realizando la descomposición en factores para poder calcular el máximo común divisor.
Método 1
Vamos a calcular el Máximo común divisor de 6 y 9.
- Escribimos todos los divisores de cada número (de 6 y de 9), anteriormente ya hemos explicado como se sacan los divisores de un número.
- Señalar todos los divisores comunes.
- Elegimos el divisor común mayor.

Método 2
Vamos a calcular el Máximo común divisor de 16 y 21.
- Factorizamos los números (16 y 21).
- Escribimos en factores cada uno de los números, el 16 y el 21.
- Ver cuáles son los factores comunes. En este caso, como ves, los números 16 y 21 no tienen factores comunes. Cuando no hay factores comunes entre los números el máximo común divisor es 1.
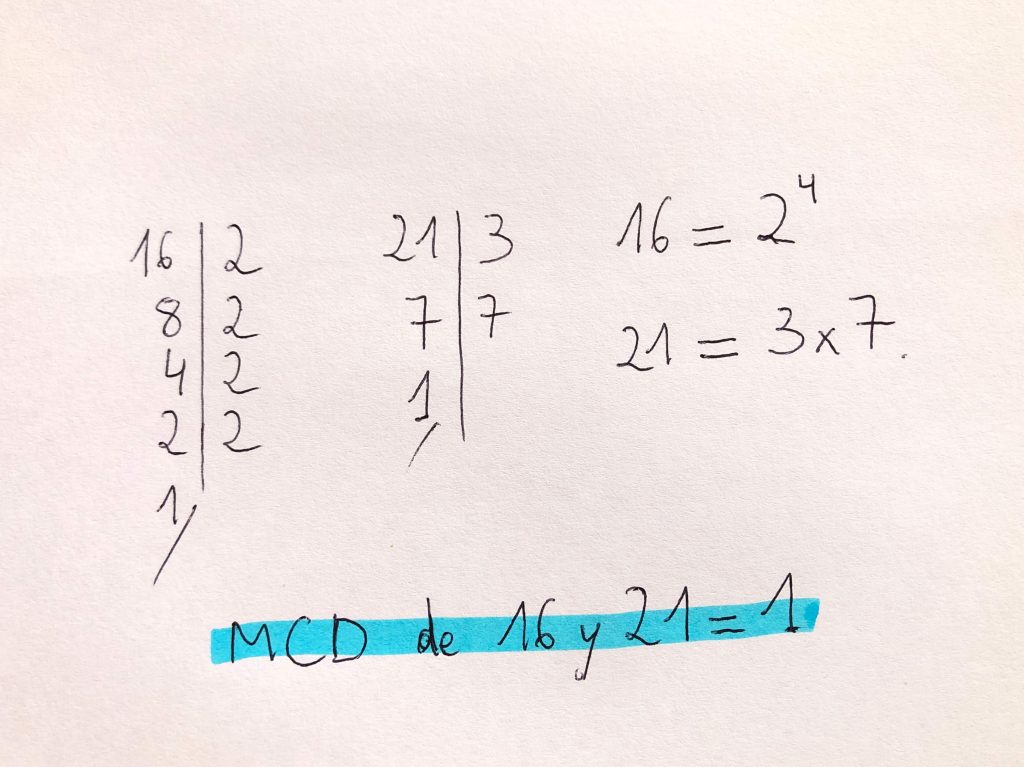
Algoritmo de Euclides extendido
El algoritmo de Euclides se puede representar con la siguiente proposición:
Sean a, b enteros no nulos. Entonces MCD(a,b)=MCD(b,r) donde r es el único 0<r<b tal que existe un entero q con a=bq+r. Esto es, que r es el resto de la división de a por b. Esta proposición nos indica que es igual de válido calcular el MCD(a,b) que el MCD(b,r), con la ventaja de que r es un entero de menor tamaño que el original a. Esto es aprovechado por el algoritmo de Euclides para el cálculo del máximo común divisor de dos números enteros.
Para calcular el mcd de dos enteros a y b (ambos >0, suponemos a>b) se definen qi y ri recursivamente mediante las ecuaciones:
a=bq1+r1 (0<r1<b)
b=r1q2+r2 (0<r2<r1)
r1=r2q3+r3 (0<r3<r2)
……..
rk−3=rk−2qk−1+rk−1 (0<rk−1<rk−2)
rk−2=rk−1qk (rk=0)
Y de la proposición anterior, se sigue que:
MCD(a,b)=MCD(b,r1)=MCD(r1,r2)=…=MCD(rk−2,rk−1)=rk−1MCD(a,b)=MCD(b,r1)=MCD(r1,r2)=…=MCD(rk−2,rk−1)=rk−1
Además se puede demostrar que el número de pasos necesarios para calcular el mcd de dos números es menor que 5 veces el número de dígitos del menor de ellos.



