¿Buscas las respuestas a todas las preguntas de desafíos matemáticos sexto grado? Estas en la página ideal! Descubre las soluciones del libro de matemáticas 6 grado contestado.
Puedes seguir haciendo scroll y encontrar las soluciones o pulsar ctrl + f (cmd + f en mac) en tu ordenador para buscar la respuesta a una pregunta que te han puesto como tarea. Te recomendamos que antes de mirar la respuesta intentes buscarla por ti mismo/a y que utilices esta página para comprobar si es correcta. Recuerda, las matemáticas también pueden ser divertidas y completar estos libro de matemáticas 6 grado te ayudaran a desarrollar la lógica.
Puedes descargar el PDF AQUÍ o consultar Teorema de Euclides, Matemáticas Primarias, Geometría o Ecuaciones.
1. Los continentes en números
Pág. 10
En equipos, escriban el nombre de los continentes ordenados de mayor a menor, primero de acuerdo con su superficie y después con su número de habitantes.
Respuestas con letra:44 900 000: Cuarenta y cuatro millones novecientos mil.42 500 000: Cuarenta y dos millones quinientos mil.30 310 000: Treinta millones trescientos diez mil.14 000 000: Catorce millones.9 900 000: Nueve millones novecientos mil.8 500 000: Ocho millones quinientos mil.
3 331 000 000: Tres mil trescientos treinta y un millones743 000 000: Setecientos cuarenta y tres millones.695 000 000: Seiscientos noventa y cinco millones.694 000 000: Seiscientos noventa y cuatro millones.27 000 000: Veintisiete millones.
2. Sin pasarse
Pág. 11
Formen equipos y completen la tabla. Usen todas las cifras permitidas.
Respuestas con letra:398 761: Trescientos noventa y ocho mil setecientos sesenta y uno.1 139 652: Un millón ciento treinta y nueve mil seiscientos cincuenta y dos.298 765 110: Doscientos noventa y ocho millones setecientos sesenta y cinco mil ciento diez.9 998 887: Nueve millones novecientos noventa y ocho mil ochocientos ochenta y siete.79 610: Setenta y nueve mil seiscientos diez.459 549 594: Cuatrocientos cincuenta y nueve millones quinientos cuarenta y nueve mil quinientos noventa y cuatro.
3. Carrera de robots
Pág. 12
Formen equipo para hacer lo siguiente. Anualmente se llevan a cabo carreras de robots en la Expo Internacional Juvenil de Robótica. Este año, el premio se entregará al equipo cuyo robot avance dando los saltos más largos, a condición de que todos sus saltos midan lo mismo. Para completar la tabla, recorten y usen el tablero de la página 181, el cual tiene los recorridos de los robots.
Robot: E. Longitud del salto: 12/4 = 3Robot: A. Longitud del salto: 8/3Robot: B. Longitud del salto: 12/5Robot: G. Longitud del salto: 10/5 = 2Robot: C. Longitud del salto: 4/2 = 2Robot: D. Longitud del salto: 7/4Robot: F. Longitud del salto: 13/8Robot: I. Longitud del salto: 7/7 = 1Robot: H. Longitud del salto: 4/5
a) ¿Cuál robot ganó la carrera?
El robot E ganó la carrera al avanzar una mayor distancia en cada salto.
b) ¿Cuáles ocuparon el segundo y el tercer lugares?
El robot A en segundo lugar y el B en tercer lugar.
c) ¿Cuál ocupó el último lugar?
El último lugar lo ocupa el robot H, ya que es el único robot que no avanza más de una unidad por salto.
5. La figura escondida
Pág. 14
Individualmente, descubre la figura escondida uniendo los puntos que están junto a cada número. Debes seguir un orden creciente (empezando por 0.001). Al final, traza una última línea que vaya del número mayor al 0.001.
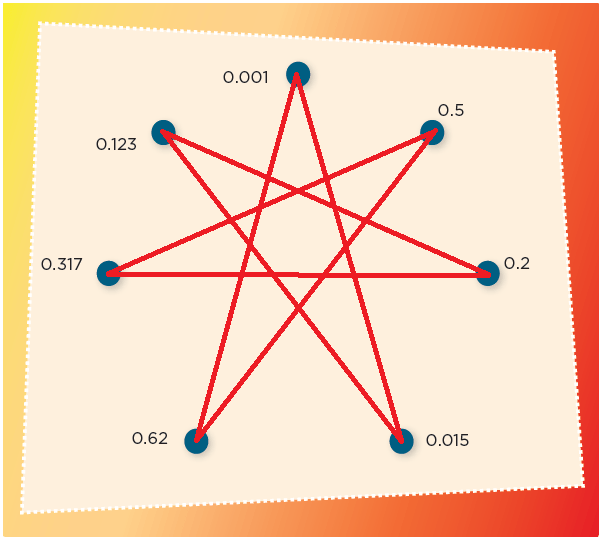
6. Vamos a completar
Pág. 15
En equipos de tres compañeros resuelvan estos problemas.1) Para comprar un juego de mesa yo aporté un quinto del total del precio, mi hermana María la sexta parte y mi papá el resto. ¿Qué parte del costo del juego aportó mi papá? Si pagamos $90, ¿cuánto dinero puso cada uno?
Su papá aportó 19/30 del total. El niño puso $18, María $15 y su papá $57.
2) ¿Qué peso pondrían en el platillo izquierdo para que la balanza se mantenga en equilibrio?
1 1/15 (un entero y un quinceavo).
Resuelve individualmente estos problemas. Cuando hayas terminado todos, reúnete otra vez con tu equipo para comparar y comentar sus resultados.1) ¿Cuánto hay que agregar a 3/4 para obtener 6/7?
3/28
2) ¿Qué tanto es menor o mayor que 1 la suma de 4/5 y 4/8?
Es mayor 3/10 que 1 ya que la suma de 4/5 y 4/8 es 1 3/10.
3) ¿Es cierto que 8/12 + 2/4 = 1 1/6?
Sí, porque al realizar la suma da como resultado 14/12 = 1 2/12 = 1 1/6
4) ¿En cuánto excede 7/9 a 2/5?
Excede quiere decir que es mayor, Lo excede en 17/45
7. Rompecabezas
Pág. 17
Reúnete con un compañero para realizar esta actividad. De las piezas blancas que están en la parte inferior, elijan las que integran correctamente cada rompecabezas.

Si en el visor de la calculadora tienes el número 0.234, ¿qué operación debes teclear para que aparezca 0.134?
Menos 0.1
Si en la calculadora tienes el número 0.234, ¿qué operación debes teclear para que aparezca 0.244?
Más 0.01
Si en la calculadora tienes el número 0.234, ¿qué operación debes teclear para que aparezca 1.23?
Más 0.996
Si en la calculadora tienes el número 0.234, ¿qué operación debes teclear para que aparezca 2.234?
Más 2
Si en la calculadora tienes el número 0.234, ¿qué operación debes teclear para que aparezca 0.24?
Más 0.006
2.¿Qué números se obtienen si a cada uno de los números de abajo sumas 0.09 y restas 0.009? 8.6
8.69 y 8.591
¿Qué números se obtienen si sumas 0.09 y restas 0.009 a 12.5?
12.59 y 12.491
¿Qué números se obtienen si sumas 0.09 y restas 0.009 a 1.25?
1.34 y 1.241
¿Qué números se obtienen si sumas 0.09 y restas 0.009 a 0.75?
0.84 y 0.741
¿Qué números se obtienen si sumas 0.09 y restas 0.009 a 1.20?
1.29 y 1.191
8. El equipo de caminata
Pág. 19
En parejas resuelvan este problema.El equipo de caminata de la escuela recorre un circuito de 4 km. El maestro está registrando en una tabla como la de abajo las vueltas y los kilómetros recorridos por cada uno de los integrantes. Analicen la tabla y complétenla.
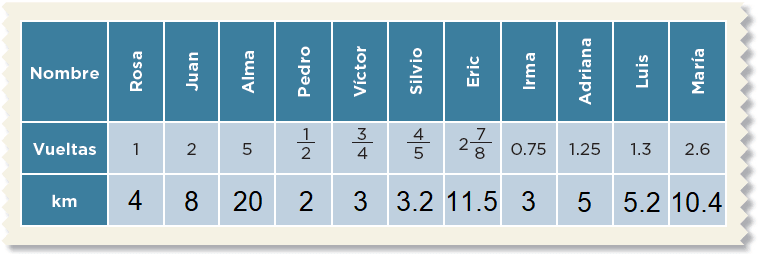
9. El rancho de don Luis
Pág. 20
En parejas, resuelvan los problemas.En el rancho de don Luis hay un terreno en el que siembran hortalizas que mide 1/2 hm. de ancho por 2/3 hm. de largo. Don Luis necesita saber el área del terreno para comprar las semillas y los fertilizantes necesarios. ¿Cuál es el área de este terreno?
2/6 = 1/3 hm²
2.En otra parte del rancho de don Luis hay un terreno de 5/6 hm. de largo por 1/4 hm. de ancho donde se cultiva durazno.¿Cuál es el área de este terreno?
5/24 hm²
10. La mercería
Pág. 21
Reunidos en equipos resuelvan el siguiente problema.Guadalupe fue a la mercería a comprar 15.5 m. de encaje blanco que necesita para la clase de costura. Si cada metro cuesta $5.60, ¿Cuánto pagó por todo el encaje que necesita?
$86.80
¿Le alcanzará el dinero para comprarla?
No le alcanza.
¿Le falta o le sobra dinero? ¿Cuánto?
Le falta $1.80
11. ¿Cómo lo doblo?
Pág. 22
Individualmente, recorta las figuras de la página 175 y 177 y después dóblalas de manera que las dos partes coincidan completamente. Marca con color el doblez o los dobleces que te permiten lograr esto.
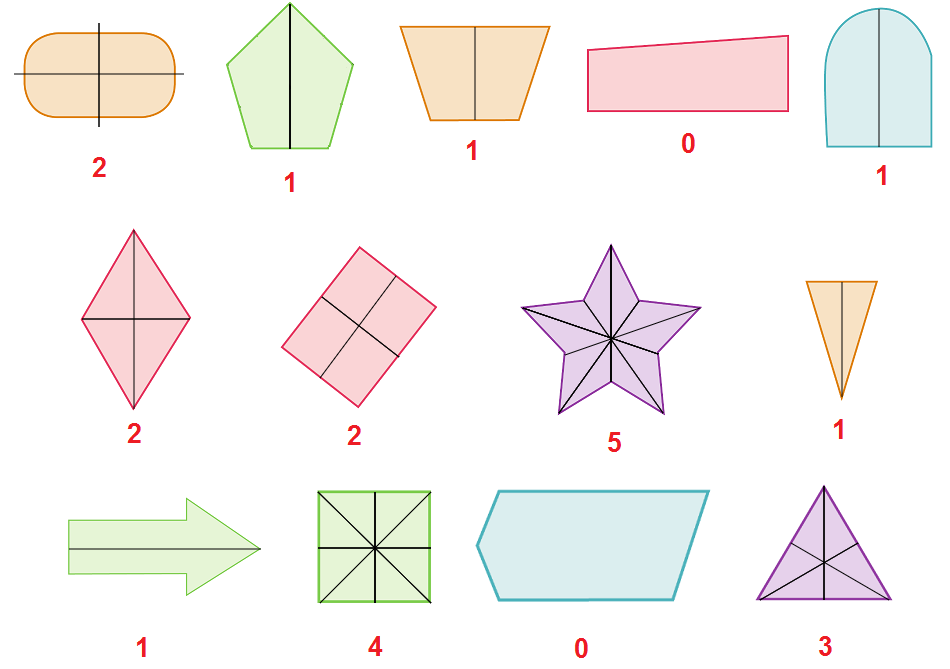
En equipos, determinen si las siguientes figuras tienen o no ejes de simetría; en caso de que los tengan, anoten cuantos son.

12. Se ven de cabeza
Pág. 23
Completa las siguientes imágenes como se indica.Individualmente, completa la imagen de modo que parezca que los dibujos se ven reflejados en el agua.
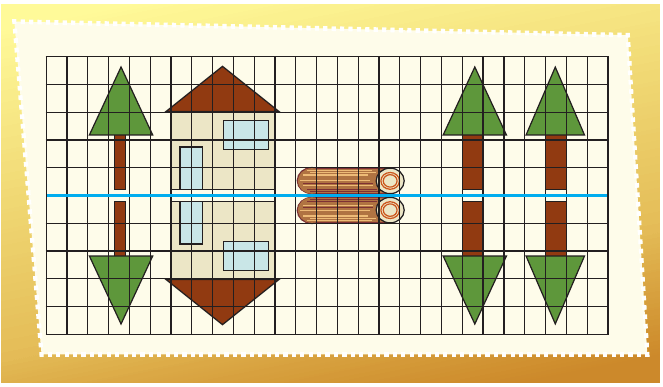
Explica qué hiciste para completar el dibujo.
Imaginamos que a partir de la línea azul hacia abajo está el agua donde se refleja la imagen de manera invertida, como si fuera un espejo. Se cuentan los cuadritos de cada figura para trazarla simétrica, es decir con las mismas medidas y forma.
2.Completa la imagen de modo que parezca que el dibujo se ve reflejado en un espejo.
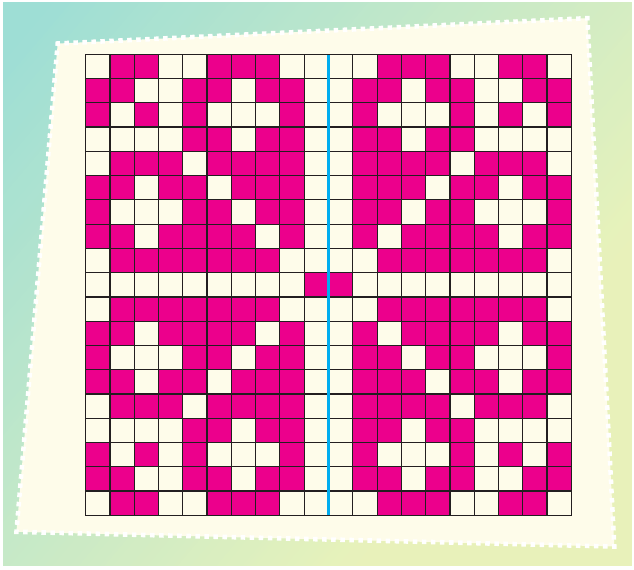
¿Crees que la imagen completa tiene más de un eje de simetría? ¿Por qué?
Sí. Porque aparte del eje de simetría vertical, tiene un eje de simetría horizontal.
3.Dibuja los pájaros necesarios para que el dibujo tenga dos ejes de simetría.
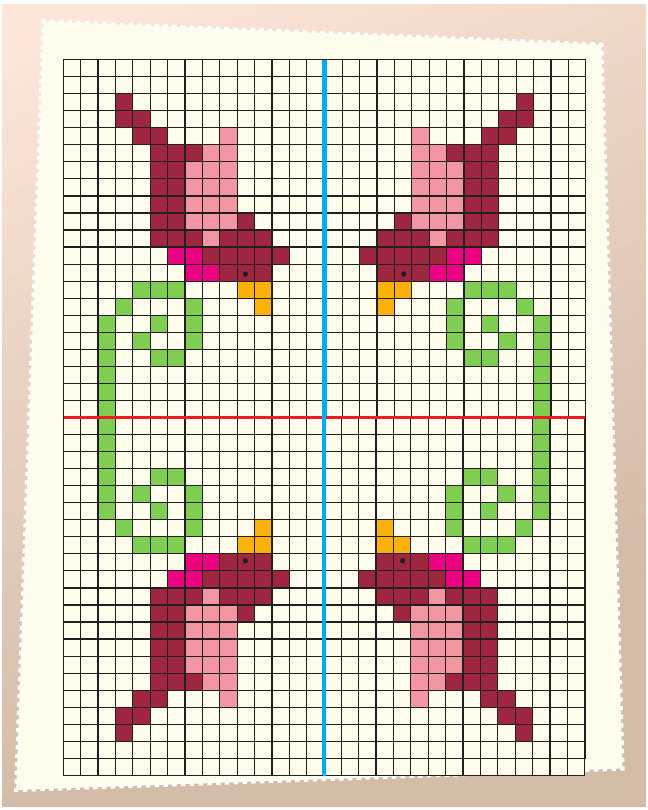
13. ¿Por dónde empiezo?
Pág. 26
a) ¿Cómo describiría Daniel a sus primos en que parte del teatro están sus lugares, si ellos no tienen el plano a la vista?
Daniel lo explicaría con sus propias palabras, pero debería empezar por decir que los lugares están en el Balcón C y que no están juntos. Luego utilizar el plano para explicarle a cada uno donde se encuentra su lugar.
b) El siguiente plano corresponde a la zona de la sección Balcón C en la cual se ubican los lugares de Daniel, Isaac, Luis, Rocío y Patricia. Márquenlos con una X, según la siguiente información.

16. Distancias iguales
Pág. 32
Ruta 1
Dar vuelta a la derecha en la calle 5 de Mayo. Seguir de frente hasta la calle 16 Oriente. Dar vuelta a la izquierda y cruzar 3 calles para llegar al punto A.
Ruta 2
Dar vuelta a la izquierda en la Avenida J. Palafox y Mendoza. Cruzar tres calles y dar vuelta a la derecha en la calle 7 Norte. Cruzar ocho calles y dar vuelta a la izquierda en la calle 16 Oriente.
Ruta 3
Dar vuelta a la derecha en la calle 5 de Mayo. Cruzar 4 calles y dar vuelta a la izquierda en la calle 8 Oriente. Cruzar 4 calles y dar vuelta a la derecha en la calle 7 Norte. Cruzar 4 calles y dar vuelta a la izquierda en la calle 16 Oriente.
17. ¿Cuál es la distancia real?
Pág. 34
En equipo, calcular la distancia real aproximada entre los siguientes cerros. De, su respuesta en kilómetros.a) De la Calavera a El Mirador.
15 km. aproximadamente. Todas la respuestas serán aproximadas, no exactas, ya que las medidas no son exactas.
b) De El Picacho a Juan Grande.
40 km. aproximadamente.
c) De San Juan a La Calavera.
35 km. aproximadamente.
d) De Los Gallos a San Juan.
40 km. aproximadamente.
18. Distancias a escala
Pág. 35
En equipos, realicen lo que se pide.Si la escala del siguiente mapa es 1:1000 000, calculen la distancia real aproximada, en kilómetros, entre los cerros:a) Grande y La Ocotera
20 km., todos los resultados son aproximados, ya que las medidas son aproximadas.
b) El Peón y Alcomún
35 km. aproximadamente.
c) Espumilla y Volcancillos
60 km. aproximadamente.
d) La Piedra Colorada y Volcán de Colima
50 km. aproximadamente.
19. Préstamos con intereses
Pág. 36
En parejas, resuelvan lo siguiente.Una casa de préstamos ofrece dinero cobrando intereses. Lo anuncia así:Te prestamos desde $100 hasta $50 000Paga un interés mensual de solamente 4%, es decir: Por cada $100 paga solo $4Calculen el interés mensual a pagar por las siguientes cantidades.
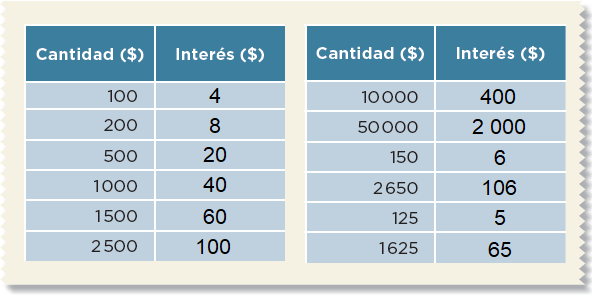
20. Mercancía con descuento
Pág. 37
En equipos, resuelvan lo siguiente.Luis, Ana y Javier venden artesanías, cada quien en su puesto del mercado. Decidieron ofrecer toda su mercancía con 10% de descuento. Completen la tabla.
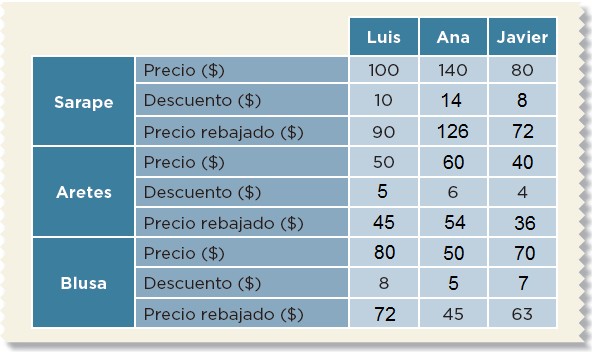
El 10% del precio de un artículo es igual a $13. Completen la siguiente tabla.
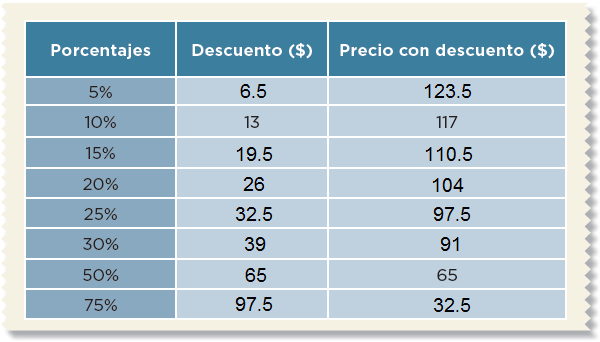
Individualmente, resuelve el siguiente problema.En un mercado de artesanías se ofrecen algunos artículos con atractivos descuentos. Completa la tabla a partir de la información disponible en ella.
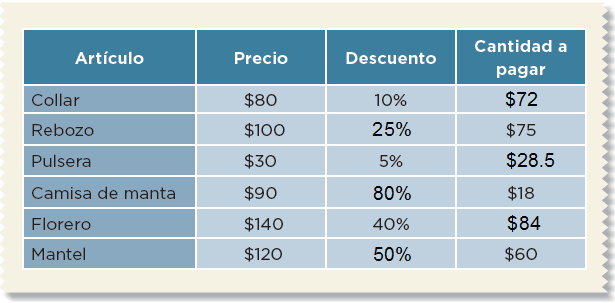
21. ¿Cuántas y de cuáles?
Pág. 39
En equipos, reúnanse para analizar, discutir y dar respuesta a las siguientes preguntas.1.En la escuela donde estudia Juan Pedro, al final de cada semana se da el reporte de ventas de paletas mediante gráficas.a) ¿Cuál sabor es el que más se vendió?
El sabor de mango.
b) ¿Cuál es el sabor que menos se vendió?
Los sabores de grosella y tamarindo.
c) Si las paletas cuestan $5, ¿cuántas paletas se vendieron?
300 paletas.
d) ¿Cuántas paletas de cada sabor se vendieron?
36 de grosella, 36 de tamarindo, 54 de uva, 75 de limón y 99 de mango.
2.En la segunda semana se presentó la siguiente gráfica.a) ¿Cuál sabor se vendió más esta semana?
El sabor limón.
b) ¿Cuál sabor se vendió menos?
El sabor uva.
c) Escribe los sabores que prefieren los niños durante la semana; ordénalos de más a menos.
Limón, grosella, mango, tamarindo y uva.
d) ¿Cuántas paletas se vendieron esta semana?
290 paletas.
3.La empresa que elabora las paletas las vende a la escuela en $3.50, ¿de cuánto ha sido la ganancia en la dos semanas?
$885
4.En el salón de Juan Pedro hay 45 alumnos y les hicieron una encuesta acerca de quiénes y cuántas paletas habían consumido en la primera semana. Observa en la tabla de la izquierda la información obtenida.¿Qué porcentaje del total de paletas fueron consumido por el grupo de Juan Pedro?
10%
22. ¡Mmm… postres!
Pág. 41
En equipos, reúnanse para analizar, comentar y resolver la siguiente actividad.En la gráfica se muestra el porcentaje y el total de ingresos mensuales por la venta de los productos en la pastelería Siempre Hay.Obtengan los datos que faltan en la tabla y complétenla.
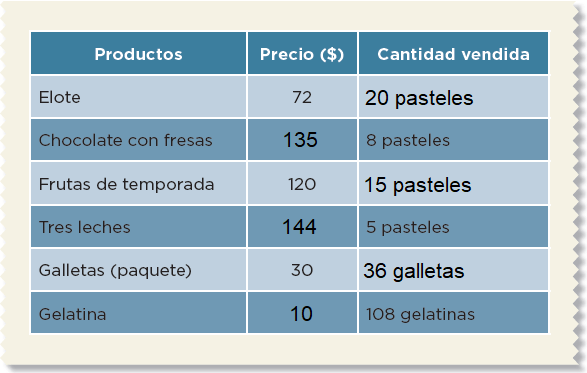
2.A partir de la información de la siguiente tabla y la anterior, respondan las preguntas.a) ¿Qué producto se vende más?
La gelatina.
b) ¿Qué producto genera mayor ingreso con menor inversión?
Galletas (paquete)
c) ¿En qué producto se invierte más y da menor ganancia?
Tres leches.
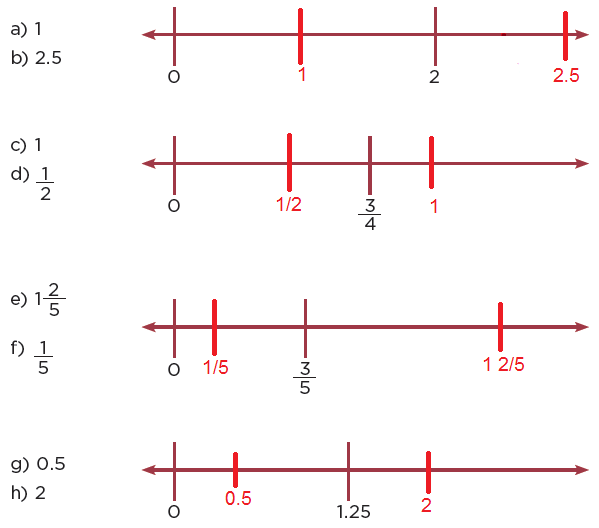
23. Sobre la recta
Pág. 44
En parejas, ubiquen en las rectas numéricas los números que se indican.
24. ¿Quién va adelante?
Pág. 45
En equipos, resuelvan el siguiente problema.En la feria de San Nicolás se lleva a cabo una carrera de 5 km. A los 20 minutos de comenzada la carrera los participantes llevan los siguientes avances.Don Joaquín, campesino, ha recorrido 1/3 del total de la carrera.
1.666 km.
Pedro, estudiante de bachillerato, ha avanzado 0.8 del recorrido.
4 km.
Juana, ama de casa, ha avanzado 1/4 del recorrido.
1.25 km.
Luisa, enfermera del centro de salud y atleta de corazón, ha recorrido 3/4 de la carrera.
3.75 km.
Mariano, alumno de primaria, lleva apenas 0.25 del recorrido.
1.25 km.
Don Manuel, ganadero, lleva 4/5 del total de la carrera.
4 km.
Luis, alumno de sexto grado, lleva 4 km. recorridos.
4 km.
a) Representen en la recta numérica las distancias recorridas por cada participante.

b) Contesten las siguientes preguntas.¿Quiénes han recorrido mayor distancia?
Pedro, Don Manuel y Luis.
¿Quiénes han recorrido menos?
Juana y Mariano.
¿Quién tiene mayor avance, el competidor que ha recorrido 4/5 o el que ha recorrido 0.8? ¿Por qué?
Ambos tienen el mismo avance. Esto debido a que 4/5 equivale a 0.8 en forma decimal.
¿Un competidor puede llevar 6/4 del recorrido? Explica tu respuesta.
No. Porque 6/4 es mayor que un entero y el recorrido finaliza cuando se recorren 5 km. de 5, lo cual se expresa como 5/5 que equivale a 1 entero.
¿Qué significa que un corredor lleve 5/5 del recorrido?
Que ha completado el recorrido.
25. ¿Dónde empieza?
Pág. 47
Formen parejas y ubiquen en las rectas numéricas los números que se indican.
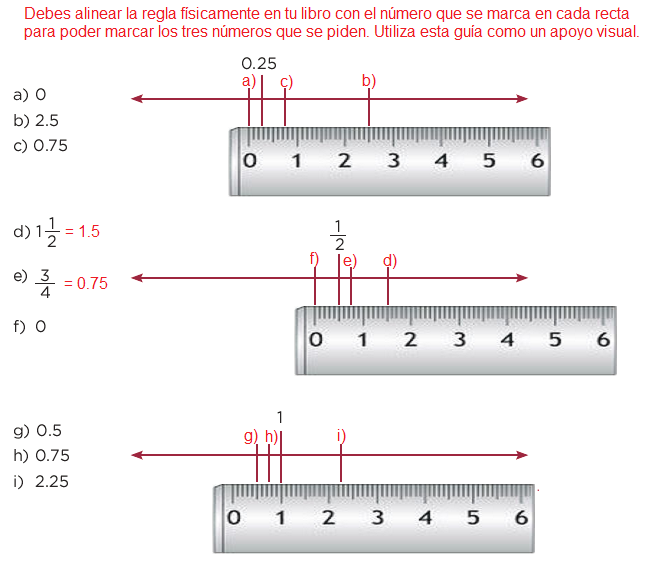
27. Por 10, por 100 y por 1 000
Pág. 50
En parejas, resuelvan estos problemas.Realicen las siguientes operaciones lo más rápido posible, sin hacer cálculos escritos.
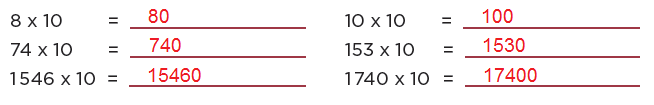
b) ¿Qué relación encuentran entre los resultados y el primer factor de cada operación?
Se le agregan al primer factor, el número de ceros que tiene el segundo factor, para obtener el resultado.
c) Escriban una conclusión relacionada con lo que observaron en sus resultados.
Cuando se multiplica un número por 100, solo se agregan 2 ceros a dicho número en el resultado.
2.¿Cuáles de estos números son el resultado de una multiplicación por 100?
400, 2 300 y 12 500
3.Completen las expresiones sin hacer cálculos escritos.
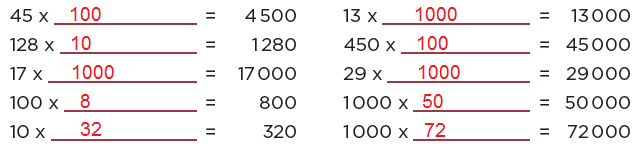
4.A partir de los resultados observados en los problemas anteriores, elaboren una regla que les sirva para resolver rápidamente multiplicaciones por 10, 100 o 1 000.
Al multiplicar un número por 10 se le agrega un 0 a dicho número, al multiplicar por 100 se agregan dos ceros y al multiplicar por 1 000 se agregan tres ceros.
Resuelvan los siguientes problemas.¿Por cuánto se tiene que multiplicar cada número para obtener el resultado de la derecha? Anoten las multiplicaciones en el espacio que corresponda.

28. Desplazamientos
Pág. 53
En parejas, hagan lo que se pide en cada caso.Al desplazar un hexágono sobre un eje vertical que pasa por su centro y unir los vértices correspondientes, se forma el siguiente cuerpo geométrico.a) ¿Cuántas caras laterales tiene?
Seis caras.
¿Qué forma tienen y cómo son entre sí?
Tienen forma hexagonal y son idénticas entre sí.
b) ¿Cuántas bases tiene el cuerpo?
Dos bases.
c) ¿Qué nombre recibe el cuerpo geométrico formado?
Pirámide hexagonal.
d) ¿Qué representa la longitud del desplazamiento del hexágono?
La altura del prisma.
2.El siguiente cuerpo geométrico se forma al desplazar sobre un eje vertical un hexágono que se va reduciendo proporcionalmente en tamaño hasta convertirse en un punto.a) ¿Cuántas caras laterales tiene?
Seis caras.
¿Qué forma tiene las caras y cómo son entre sí?
Tienen forma triangular y son idénticas entre sí.
b) ¿Cuántas bases tiene?
Una base.
d) ¿Qué representa la longitud del eje de desplazamiento del hexágono?
La altura de la pirámide.
3.Utilicen una regla o escuadra para terminar de dibujar los siguientes prismas y pirámides. Escriban su nombre completo de acuerdo con la forma de sus bases.

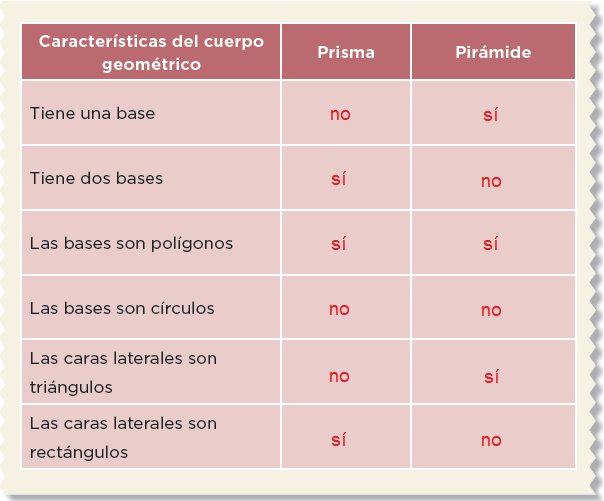
4.Escriban las características que diferencian a los prismas de las pirámides.
Los prismas cuentan con 2 bases y caras rectangulares. Mientras que las pirámides cuentan con una sola base y sus caras son triangulares.
5.De acuerdo con lo anterior, escriban las definiciones de:a) Prisma:
Cuerpo geométrico con 2 bases iguales y caras laterales en forma de rectángulo.
b) Pirámide:
Cuerpo geométrico con 1 sola base y caras laterales en forma de triángulo que coinciden en un punto llamado ápice.
c) Altura de un prisma:
Es la distancia entre sus 2 bases.
d) Altura de una pirámide:
Segmento perpendicular a la base que une su centro con el punto más alto (ápice).
29. ¿En qué son diferentes?
Pág. 57
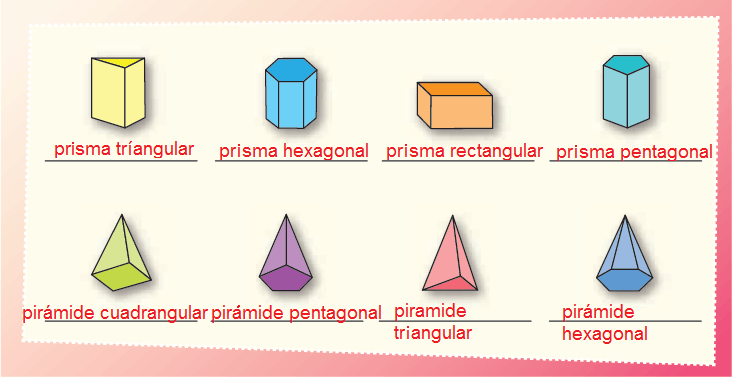
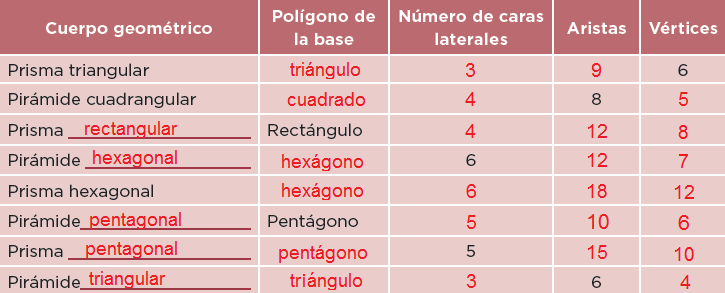
En equipos, hagan lo que se pide a continuación.Escriban sobre la línea el nombre de cada cuerpo geométrico.
2.Anoten los datos que hacen falta en la siguiente tabla.
3.Escriban Sí o No, según corresponda.
31. Ofertas y descuentos
Pág. 60
En equipos, resuelvan los siguientes problemas.Pepe logró ahorrar $500 y con ese dinero decidió comprar un reloj que costaba $450.00; al pagarlo, se enteró que tenía un descuento. ¿Qué porcentaje le descontaron, si al salir de la tienda aún tenía $140.00 de sus ahorros?
20% de descuento.
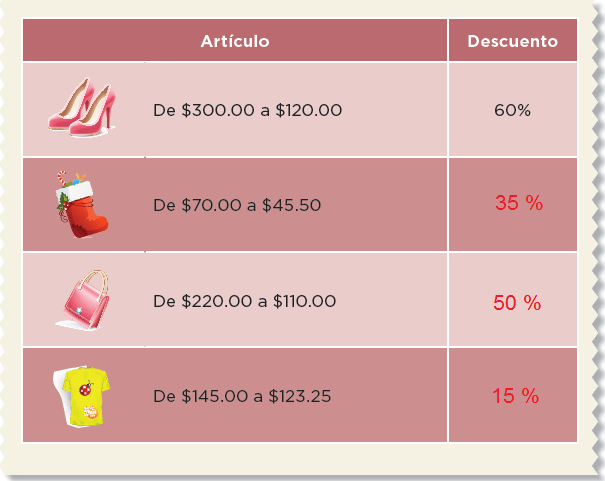
2.En la tienda donde Felipe compró su reloj, había otros artículos con descuento, pero la etiqueta sólo indicaba el precio de lista y el precio rebajado. Encuentra los porcentajes de descuento y regístralos en la tabla.
32. El IVA
Pág. 61
En equipos, resuelvan los siguientes problemas. Pueden auxiliarse con su calculadora.El precio de una refacción es de $240.00. A esta cantidad se debe agregar 16% de IVA. ¿Cuál es el precio de la refacción con el IVA incluido?
$278.40
2.Otra refacción cuesta $415.28 con el IVA incluido. ¿Cuál es el precio de la refacción sin el IVA?
$358.00
33. Alimento nutritivo
Pág. 62
a) El ácido fólico ayuda a la buena formación de las células sanguíneas. ¿Qué le conviene más a una mujer embarazada: tomar leche fortificada o sin fortificar?
Fortificada.
¿Por qué?
Porque la leche Alfa fortificada aporta 20.4 mg. más de ácido fólico que la leche sin fortificar.
b) ¿Cuánta energía proporciona un vaso de leche de 250 ml.?
148 kcal.
c) ¿Cuál es la cantidad de leche que se recomienda tomar diariamente?
400 ml.
d) La vitamina C ayuda al sistema inmunológico. ¿Qué tipo de leche es más recomendable para ayudar en el tratamiento de enfermedades infecciosas?
La leche Alfa fortificada.
e) ¿Qué significa que la leche esté fortificada?
Que tiene una mayor cantidad de nutrientes.
a) ¿Qué tipo de arroz aporta más vitamina B1?
El arroz integral.
b) ¿Qué tipo de arroz proporciona mayor cantidad de yodo al organismo?
El arroz refinado.
c) ¿Qué tipo de arroz aporta mayor cantidad de fibra?
El arroz integral.
d) El complejo B (formado por diferentes vitaminas tipo B) ayuda al mejor funcionamiento del sistema nervioso. ¿Cuántos miligramos de este complejo aporta el arroz refinado?
5.16 mg.
e) La deficiencia de potasio en el organismo puede causar debilidad muscular. El cuerpo de una persona mayor de 10 años requiere una cantidad aproximada de 2 000 mg. al día. ¿Qué tipo de arroz es preferible que consuma una persona? Explica tu respuesta.
El arroz integral, ya que contiene el doble de potasio que el arroz refinado.
f) ¿Qué tipo de arroz es preferible comer? Explica tu respuesta.
El arroz integral porque ofrece hasta el doble de nutrientes que el refinado y tiene menos calorías.
34. Nuestro país
Pág. 66
a) ¿Cuál es la extensión del territorio mexicano?
1 964 375 km².
b) ¿En qué orden se organizaron los datos de la tabla?
Descendente. Del país más extenso al menos extenso.
c) ¿Qué lugar ocupa México por la extensión de su territorio?
Lugar 14.
d) ¿Cuál es el país más grande del mundo?
La Federación Rusa.
e) ¿Cuántos y cuáles países de América se encuentran entre los más grandes del mundo?
Los primeros tres son Canadá, Estados Unidos y Brasil.
f) ¿Qué lugar ocupa México entre los países de América con base en su extensión territorial?
Quinto.
g) Muchas veces se dice que México tiene una superficie de 2 000 000 km². ¿Por qué creen que se diga eso?
Porque se redondea la extensión al entero más cercano o próximo.
h) ¿Qué lugar ocupa su entidad con respecto al número de habitantes?
Selecciona tu entidad y observa los datos de la gráfica de página 69.
i) ¿Qué entidades tienen menos de un millón de habitantes?
Baja California Sur, Campeche, Colima y Tlaxcala.
j) ¿Consideran que el número de habitantes es proporcional a la extensión territorial de la entidades?¿Por qué?
Si, porque a mayor extensión territorial, mayor población, casi en el total de las entidades.
a) ¿Cuál es la entidad federativa con mayor extensión territorial?
Chihuahua.
b) ¿Cuál es la entidad más pequeña?
Tlaxcala..
c) La entidad en que viven, ¿qué lugar ocupa de acuerdo con el tamaño de su territorio?
Se anotan todas las entidades para que les sirva a todos las respuestas.1) Chihuahua 247 087, 2) Sonora 184 934, 3) Coahuila 151 571, 4) Oaxaca 95 364, 5) Jalisco 80 137, 6) Tamaulipas 79 829, 7) Zacatecas 75 040, 8) Chiapas 73 887, 9) Baja California Sur 73 677, 10) Durango 73 677, 11) Veracruz 72 815, 12) Baja California 70 113, 13) Nuevo León 64 555, 14) Guerrero 63 794, 15) San Luis Potosí 62 848, 16) Michoacán 59 864, 17) Sinaloa 58 092, 18) Campeche 51 833, 19) Quintana Roo 50 350, 20) Yucatán 39 340, 21) Puebla 33 919, 22) Guanajuato 30 589, 23) Nayarit 27 621, 24) Tabasco 24 661, 25) Estado de México 21 461, 26) Hidalgo 20 987, 27) Querétaro 11 769, 28) Aguascalientes5 589, 29) Colima 5 455, 30) Morelos 4 941, 31) Tlaxcala 3 914 y 32) Distrito Federal 1 499
d) ¿Cuáles son los tres estados más grandes de la república mexicana?
Chihuahua, Sonora y Coahuila.
e) ¿Qué entidades tienen menos de 10 000 km²?
Aguascalientes, Colima, Distrito Federal, Morelos y Tlaxcala.
f) ¿Qué entidad tiene mayor población?
El Estado de México.
g) ¿Cuál es la entidad con menor número de habitantes?
Tlaxcala.
35. ¿Quién es el más alto?
Pág. 72
En equipos, analicen la siguiente situación y contesten lo que se pide.A los alumnos de un grupo de sexto grado se les solicitó la medida de su estatura. Los únicos que la sabían la registraron de la siguiente manera: Daniel, 1.4 m.; Alicia, un metro con 30 cm.; Fernando 1 1/4 m.; Mauricio, 1.50 m.; Pedro, metro y medio; Sofía 1 1/5 m. y Teresa dijo que medía mas o menos 1.50 m.a) ¿Quién es el más bajo de estatura?
Sofía.
b) ¿Hay alumnos que miden lo mismo?
Sí.
¿Quiénes?
Mauricio y Pedro miden 1.50 m.
c) Teresa no sabe exactamente su estatura, pero al compararse con sus compañeros se da cuenta de que es más alta que Daniel y más baja que Pedro. ¿Cuánto creen que mide?
Mide entre 1.40 y 1.50 metros.
36. ¿Cuál es el sucesor?
Pág. 73
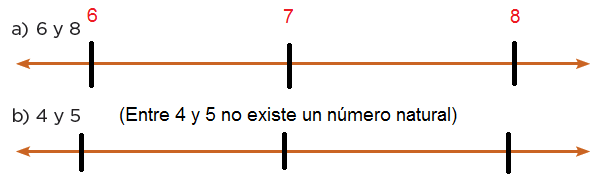
En parejas, lleven a cabo las siguientes actividades.Representen en una recta numérica los números naturales indicados e identifiquen entre ellos un tercer número natural.
2.Representen en una recta numérica los números decimales indicados e identifiquen entre ellos un tercer número decimal.
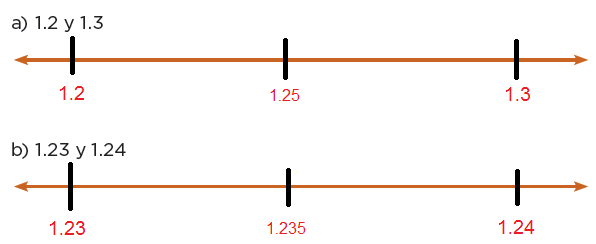
3.Con base en las actividades anteriores, respondan las siguientes preguntas.a) ¿Cuál es el sucesor de 6?
Siete.
b) ¿Todos los números naturales tienen un sucesor?
Sí.
¿Por qué?
Porque después de cada decimal existen un infinito número de sucesores.
c) ¿Cuál es el sucesor de 1.2?
Puede ser el 1.21, el 1.201 o el 1.211, etc. Los números decimales no tienen un sucesor definido.
d) ¿Todos los números decimales tienen un sucesor?
No tienen un sucesor definido.
37. Identifícalos fácilmente
Pág. 75
En equipos, analicen la siguiente tabla. Después, completen los espacios en blanco y respondan lo que se pide.
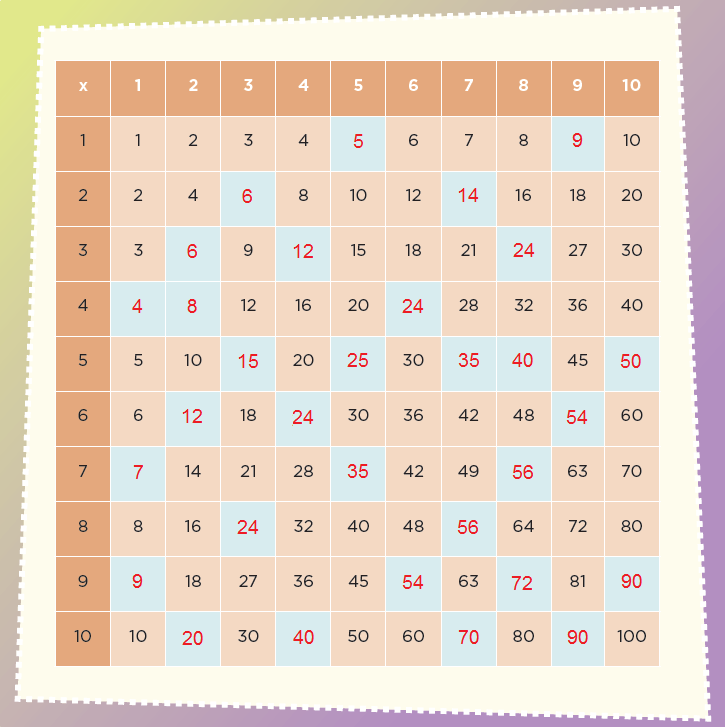
a) Escriban cómo encontraron los números faltantes de la tabla y comenten si de esa forma podrían encontrar más números para nuevas filas y columnas.
Cada número dentro de la tabla es el resultado de multiplicar la fila por la columna que le corresponden.Las filas se presentan de manera horizontal (de izquierda a derecha) y las columnas de manera vertical (de arriba hacia abajo).Se pueden encontrar más números para nuevas filas y columnas.
b) ¿Qué característica tienen en común todos los números de la fila o columna del 2?
Todos son múltiplos de 2.
c) ¿Con qué cifras terminan los números de la fila o columna del 5?
Terminan en 0 ó 5.
¿Qué tienen en común los números de la fila del 10?
Terminan en 0 y son múltiplos de 10.
En equipo, completen los esquemas con los números de la tabla de la página 75. Consideren que el resultado de multiplicar dos números siempre es múltiplo de ellos.
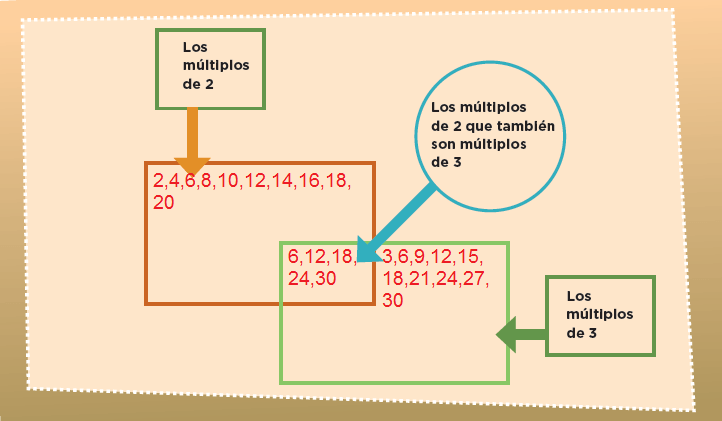
Completen los esquemas con los números de la tabla anterior.
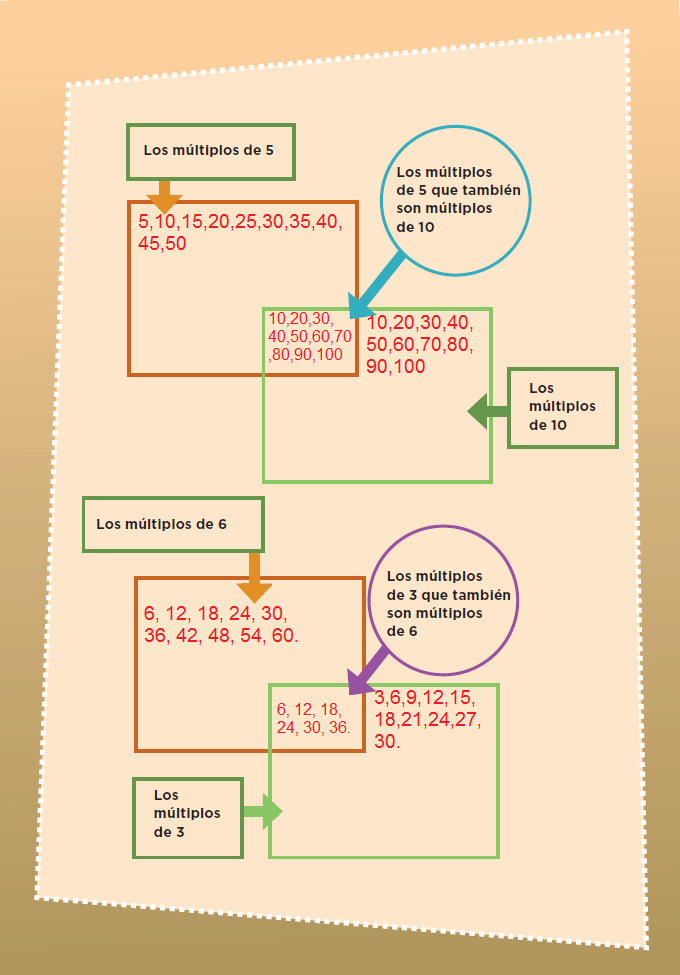
38. ¿De cuánto en cuánto?
Pág. 79
En parejas, realicen lo que se indica.a) Escriban cinco múltiplos de 10 mayores que 100.
110, 120, 130, 140 y 150.
b) Escriban cinco múltiplos de 2 mayores que 20.
22, 24, 26, 28 y 30.
c) Escriban cinco múltiplos de 5 mayores que 50.
55, 60, 65, 70 y 75.
d) Escriban cinco múltiplos de 3 mayores que 30.
33, 36, 39, 42 y 45.
Contesten las siguientes preguntas.a) ¿El número 48 es múltiplo de 3?
Sí.
¿Por qué?
Porque al dividir 204 entre 6, obtenemos un resultado exacto.
b) ¿El número 75 es múltiplo de 5?
Sí.
¿Y el 84?
No.
c) ¿El número 850 es múltiplo de 10?
Sí.
¿Y de 5?
Sí.
d) ¿El número 204 es múltiplo de 6?
Sí.
Comenten y contesten lo que se indica.Carmen y Paco juegan en un tablero cuadriculado, cuyas casillas están numeradas del 1 al 100; ella utiliza una ficha verde que representa un caballo que salta de 4 en 4, y él una ficha azul que representa a otro que salta de 3 en 3.a) ¿Puede haber una trampa (casilla) entre el 20 y 25 en la que caiga alguno de los dos caballos?
Sí. Los caballos pueden caer en la trampa (casilla) 24.
Argumenten su respuesta.
El número 12 es múltiplo común de 3 y 4. Múltiplo común quiere decir que es múltiplo de los dos, de 3 y de 4, por esa razón, los dos caballos, el representado por la ficha verde y el representado por la ficha azul caerán en la trampa (casilla) 12.
b) ¿Habrá alguna casilla entre el 10 y 20 donde puedan caer los dos?
Sí. En la 12.
c) ¿En qué casilla caerán los dos?
12, 24, 36, 48, 60, 72, 84 y 96
Forma pareja con otro compañero y hagan lo que se indica.Coloquen los números que están en la parte inferior de cada recuadro, de tal modo que las afirmaciones sean verdaderas.
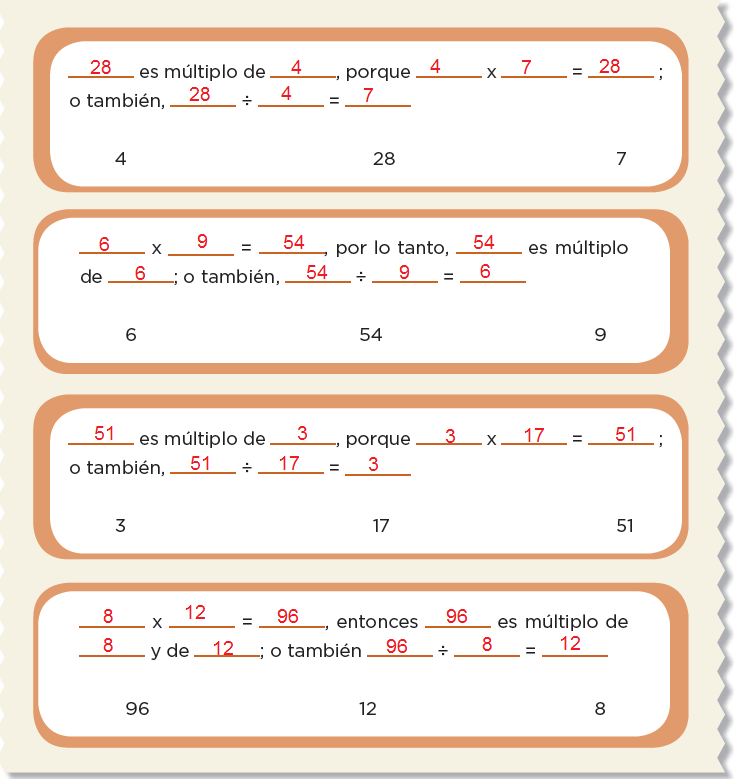
40. El número venenoso y otros juegos
Pág. 84
Después de jugar, respondan estas preguntas: si lo requieren, pueden usar calculadora.a) De acuerdo con las reglas del juego, si el equipo sigue contando después de 120, ¿se debe decir en voz alta el número 150 o dar una palmada?
Según las reglas, el reto termina al llegar el equipo al número 120. Si se continuara el juego, después del 120, en el número 150 se debe dar una palmada.
¿Por qué?
Porque al dividir 468 entre 4 nos da:468 ÷ 4 = 117, el resultado es exacto, por lo tanto 468 es múltiplo de 4.
b) ¿Y el 580?
Recordemos que el reto termina al llegar al número 120, pero si se continuara jugando, el 580 se dice en voz alta porque no es múltiplo de 6.
c) ¿Y el 3 342?
Recordemos que el reto termina al llegar al número 120, pero si se continuara jugando, en el 3 342 se da una palmada porque es múltiplo de 6.
d) Digan un número mayor a 1 000 al que le corresponda una palmada. ¿Cómo lo encontraron?
1 002, porque al dividirlo entre 6 da167, es decir, un resultado exacto.
2.Ahora van a cambiar de juego. Continúen con sus mismos compañeros de equipo. Al terminar, respondan las preguntas.En el equipo organicen parejas; decidan cual comenzará el juego.Los dos integrantes de la pareja, en voz alta y al mismo tiempo, contarán de 4 en 4 a partir de 0, hasta que alguno se equivoque. El resto del equipo llevará la cuenta de cuántos números lograron decir. La pareja que logre más números será la ganadora.a) En caso de que alguna pareja pueda continuar sin error, ¿dirá en algún momento el 106?
No.
b) ¿Dirá el 256?
Sí.
c) ¿Y el 310?
No.
d) ¿Y el 468?
Sí.
e) Digan un número mayor a 1 000 que la pareja debería decir si no se equivocara. ¿Cómo lo encontraron?
El 1 004, porque al dividirlo entre 4 = 251, el resultado es exacto.
3.Ahora, formen un equipo con otros compañeros.Todos tomen su calculadora y tecleen.a) ¿Qué números aparecen?
3, 6, 9, 12, 15 y 18
b) Si continúan tecleando el signo de igual (=), ¿aparecerá en la pantalla de la calculadora el 39?
Sí.
¿Cómo lo saben?
Al realizar la división: 1 532 ÷ 3 = 510.666, no da un resultado exacto, por lo tanto 1 532 no es múltiplo de 3.
c) ¿Aparecerá el 300?
Sí
d) ¿Y el 1 532?
No.
e) Digan un número mayor que 2 000 que sí aparecerá en la pantalla. ¿Cómo lo encontraron?
El 2001.Se le suma de 1 en 1 al 2 000 y se divide entre 3, hasta encontrar el primer múltiplo de 3, mayor que 2 000.
Formen equipos y jueguen los siguientes dos juegos.¡Piensa rápido y resuelve!
a) Explica por qué 3 es divisor de 75.
Porque la división de 75 entre 3 es exacta.
b) Explica por qué 8 no es divisor de 75.
Al realizar la división 75 entre 8 no resulta una división exacta. Es una división que tiene residuo.
c) Anota todos los divisores de 18.
1, 2, 3, 6, 9 y 18.
d) ¿De cuáles números mayores que 1 979 y menores que 2 028 es divisor el número 25?
Del 2 000 y del 2 025.
2.Completen la siguiente tabla.
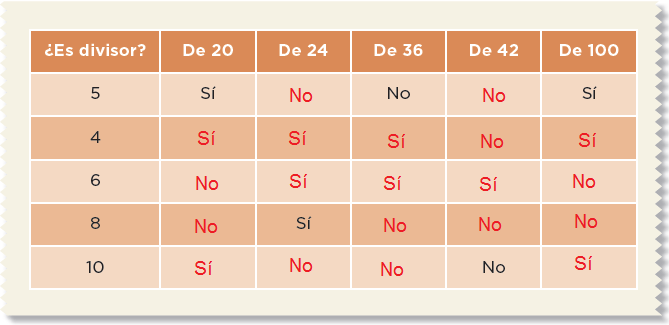
3.Adivina, adivinador.a) Adivina, adivinador, soy divisor de 4 y 6; si no soy el 1, ¿qué número soy?
2
b) Adivina, adivinador, soy un número mayor que 10 y menor que 20; además, de 24 y 48 soy divisor, ¿qué número soy?
12
41. ¿Dónde están los semáforos?
Pág. 90
En equipos, observen el siguiente croquis y respondan las preguntas.La ubicación del semáforo 3 está determinada por el par de números ordenados (7,2).a) ¿Cuáles son los pares ordenados que corresponden a la ubicación de los otros semáforos?
Semáforo 1: (5, 8)Semáforo 2: (3, 4)Semáforo 4: (1, 7)Semáforo 5: (10, 5)
b) Ubiquen un sexto semáforo en (5,6) y otro más en (1,9)
(5,6), cinco cuadras en la calle horizontal y seis en la calle vertical.(1,9), una cuadra en la calle horizontal y nueve en la calle vertical.
42. Un plano regular
Pág. 91
En parejas, realicen lo que se pide a continuación; si es necesario, utilicen el plano cartesiano.a) Recorten el plano cartesiano de la página 161 y ubiquen en él los puntos (3, 0), (8, 0) y (5, 0).
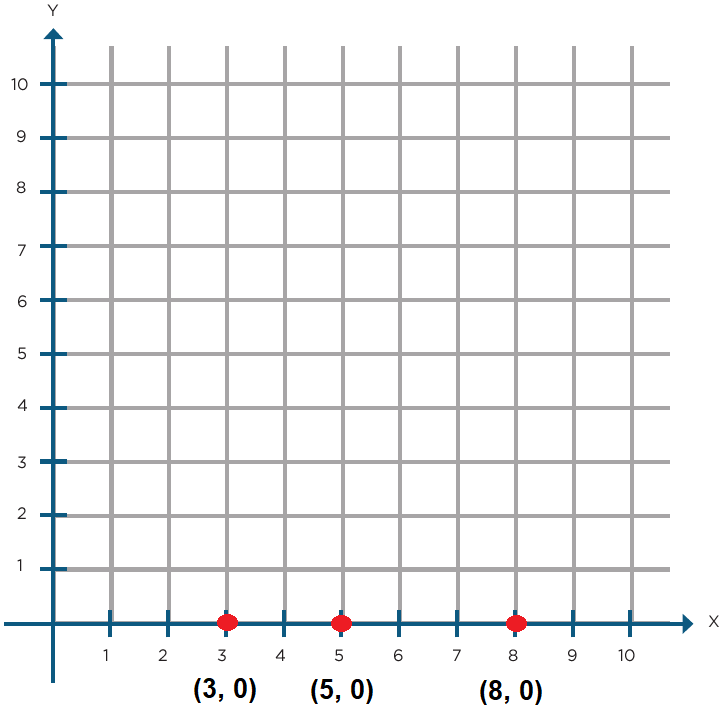
b) ¿Qué características tienen las coordenadas de 5 puntos que se ubican sobre el eje horizontal?
El segundo número del par de coordenadas (ordenadas) siempre será 0.
c) ¿Qué características tienen las coordenadas de los puntos que se ubican sobre una paralela al eje horizontal?
El segundo número del par de coordenadas (ordenadas) siempre será el mismo.
d) Ubiquen los puntos (5, 8), (5, 2) y (5, 6) y únanlos.
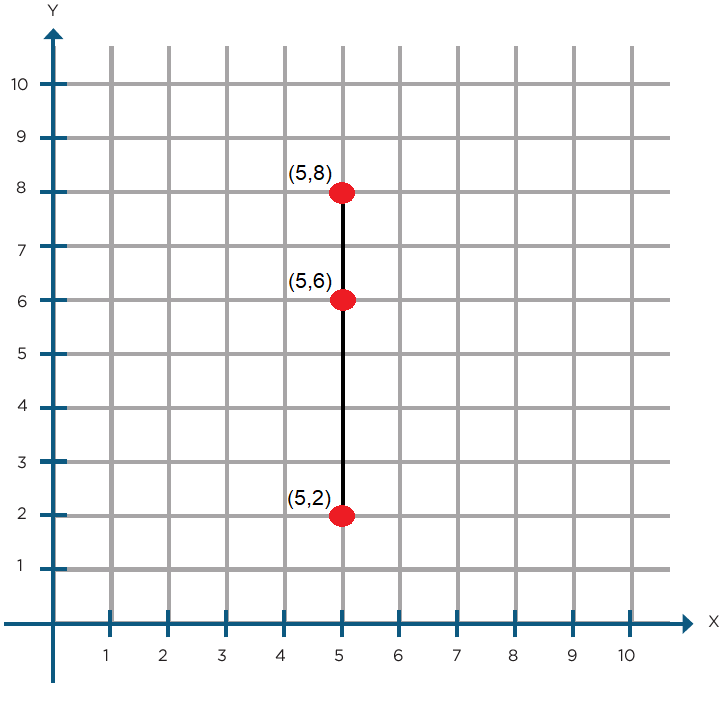
e) Sumen 1 a las abscisas de los puntos del inciso d, localícenlos en el plano cartesiano y únanlos. ¿Qué sucede?
Se forma una recta paralela a la anterior.
f) Mencionen las características que deben tener todos los pares ordenados que se ubican en una recta paralela al eje vertical o paralela al horizontal.
Los pares ordenados paralelos al eje vertical comparten el mismo número en las abscisas y los pares ordenados paralelos al eje horizontal comparten el mismo número en las ordenadas.
43. Hunde al submarino
Pág. 92
Formen parejas para jugar a Hunde al submarino. Recorten el tablero y los submarinos de la página 159 y sigan las reglas que se dan a continuación.
Con las instrucciones y con los recortables realicen esta actividad.
Formen parejas y jueguen. Traza la figura geométrica con las siguientes reglas.
Con las instrucciones realizar la actividad.
44. Pulgada, pie y milla
Pág. 95
En equipos resuelvan los siguientes problemas.Don Juan fue a la ferretería a comprar una manguera para regar su jardín. Después de observar varias, eligió una que tiene la siguiente etiqueta.a) ¿Cuántos metros de longitud tiene la manguera que compró don Juan?
25.2984 m.
b) ¿Cuántos centímetros de diámetro interior tiene la manguera?
1.27 cm.
2.El siguiente dibujo representa el velocímetro del automóvil de don Juan¿Cuál es la velocidad máxima en kilómetros de su automóvil?
225.3076 km/h
45. Libra, onza y galón
Pág. 96
En parejas, resuelvan el siguiente problema.Los padres de Luis le están organizando una fiesta de cumpleaños. Ayúdenles a seleccionar la presentación de galletas y de jugos que más convenga, considerando su precio y contenido.
Jugos: la presentación 1 es la más económica.
46. Divisas
Pág. 97
En parejas, resuelvan lo siguiente.El 11 de noviembre de 2008, en la sección financiera de un diario de circulación nacional apareció una tabla con los precios de venta de varias monedas extranjeras. Con base en ella, contesten lo que se pide.a) ¿Cuántos pesos se necesitan para comprar 65 dólares?
$885.95
b) ¿Cuántos yenes se pueden comprar con 200 pesos?
1 098.90 yenes
c) ¿A cuántos euros equivalen 500 dólares?
389.20 euros
47. ¿Cuántos de éstos?
Pág. 98
En equipos, resuelvan el siguiente problema.Con 24 cajas de pañuelos desechables se puede formar una caja grande, tal como se muestra en el dibujo. Dibujen otra que requiera la misma cantidad de cajas, pero organizadas de forma diferente.
¿Tendrá el mismo volumen que la anterior?
Si.
49. ¿Cuál es el mejor precio?
Pág. 101
En equipos, resuelvan los siguientes problemas sin hacer operaciones. Argumenten sus respuestas.El paquete A tiene 5 panes y cuesta $15, el paquete B tiene 6 panes y cuesta $12. ¿En qué paquete el pan es más barato?
Paquete B.
2.En la papelería, una caja con 15 colores cuesta $30 y en la cooperativa de la escuela, una caja con 12 colores de la misma calidad cuesta $36. ¿En qué lugar es preferible comprar los colores?
En la papelería.
3.El paquete de galletas A cuesta $6 y contiene 18 piezas. El paquete B contiene 6 galletas y cuesta $3. ¿Qué paquete conviene comprar?
El paquete A.
4.En el mercado, un kilogramo de naranjas consta de 9 piezas y cuesta $10. En la huerta de don José, 8 naranjas llegan a pesar un kilogramo y cuestan $8. ¿En dónde conviene comprar las naranjas?
En la huerta de don José.
50. ¿Cuál está más concentrado?
Pág. 102
En equipos, resuelvan los siguientes problemas.Se preparó una naranjada A con 3 vasos de agua por cada 2 de jugo concentrado. Además, se preparó una naranjada B con 6 vasos de agua por cada 3 de jugo. ¿Cuál sabe más a naranja?
Naranjada A.
2.Para pintar la fachada de la casa de Juan se mezclan 4 litros de pintura blanca y 8 litros de pintura azul. Para pintar una recámara se mezclan 2 litros de pintura blanca y 3 litros de pintura azul. ¿En cuál de las dos mezclas es más fuerte el tono azul?
En la mezcla de la recámara.
51. Promociones
Pág. 103
En equipos, resuelvan los siguientes problemas.1.En la ciudad donde vive Carlos se instaló una feria y en uno de los puestos se ofrece una promoción: ganar 2 regalos si se acumulan 10 puntos. En otro dan 3 regalos por cada 12 puntos ¿Cuál puesto tiene la mejor promoción?
En el segundo puesto.
2.En la feria se anunciaron más promociones. En los caballitos, por cada 6 boletos comprados se regalan 2 más. En las sillas voladoras, por cada 9 boletos comprados se regalan 3. ¿En qué juego se puede subir gratis más veces?
En ambos juegos se puede subir gratis las mismas veces.
52. La edad más representativa
Pág. 104
Trabajen en equipo para resolver lo que se indica a continuación. En una reunión hay 9 personas. Sus edades, en años, son las siguientes.¿Cuál es la media aritmética (promedio) de las edades?
37.111 años.
¿Qué procedimiento utilizaron para encontrarla?
Sumando todas las edades y dividiendo el resultado entre el número de personas.
2.Ordenen las edades de menor a mayor y localicen el valor del centro. ¿Cuál es ese valor?
28
3.El valor que definieron en la pregunta anterior es la mediana. Entre este valor y la media aritmética o promedio, ¿cuál consideran que es más representativo de las edades de las personas?
La mediana.
Argumenten su respuesta.
La mediana (28) es la más representativa ya que es cercana a la mayoría de las edades del grupo.
54. México en números
Pág. 107
En equipos, analicen y decidan, en cada problema. cuál es la medida de tendencia central más conveniente para dar una información representativa de cada conjunto de datos. Expliquen por qué lo consideraron así y calcúlenla,La información que el Inegi recaba a partir de los Censos Nacionales de Población y Vivienda y los Conteos de Población es analizada y organizada por temas para obtener estadísticas sociodemográficas de México. Algunos datos interesantes son:1.Distribución de la población en México. La tabla muestra, de la población total de cada entidad, el porcentaje que vive en zonas urbanas.Datos para analizar y decidir en equipo cuál es la medida de tendencia central más conveniente para dar una información representativa de cada conjunto de datos.
Moda 84, 86, 87 y 88; Mediana 86; Promedio 85.142
De este conjunto de datos, ¿será más representativa la moda, la mediana o la media aritmética?
Todas son representativas, porque están muy cerca del centro y entre ellas casi no hay diferencia..
¿Por qué?
Por aproximarse a la mayoría de los valores del grupo.
De este conjunto de datos, ¿cuál de las tres medidas estudiadas (media aritmética, mediana o moda) es la más representativa?
La moda y mediana.
De este conjunto de datos, ¿cuál de las tres medidas estudiadas (media aritmética, mediana o moda) es la más representativa?¿Por qué?
Debido al rango tan variable de los elementos del grupo.
55. Los jugos
Pág. 112
En parejas, de acuerdo con la siguiente publicidad sobre diferentes marcas de jugos, hagan lo que se indica.Completen la tabla anotando el costo que se ve en el envase. Si no existe esa presentación, dejen vacío el espacio.
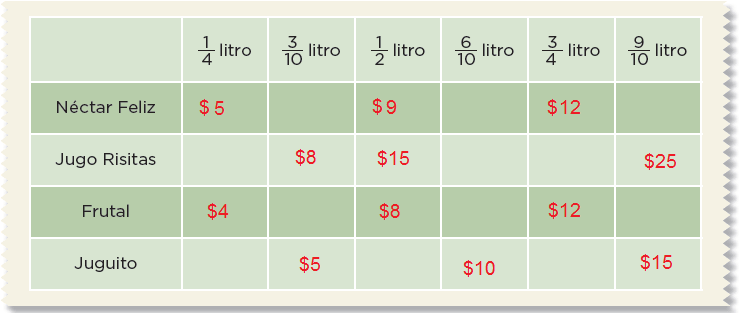
Juan dice que 0.3 litros equivalen a 1/3 (un tercio) de litro. ¿Están de acuerdo con él?
No.
Argumenten su respuesta.
0.3 = 3/101/3 = 1 ÷ 3 = 0.3333333333…Si bien 1/3 es cercano o próximo a 0.3 no equivale exactamente a esa cantidad.
56. Los listones 1
Pág. 113
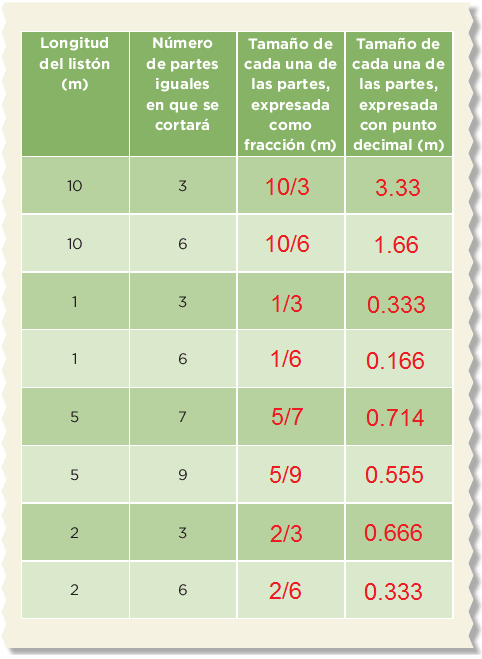
Se tienen algunos listones que deben ser divididos en partes iguales. En equipos, completen la tabla; deben anotar el tamaño de cada parte en metros.

57. Los listones 2
Pág. 114
Se tienen algunos listones de diferente longitud que deben ser cortados en partes iguales. En equipos, completen la tabla (recuerden dar el tamaño de las partes en metros).
58. ¿Cómo va la sucesión?
Pág. 115
En equipos, resuelvan los siguientes problemas. Pueden utilizar su calculadora.1.Si una sucesión aumenta de 1.5 en 1.5, ¿cuáles son los primeros 10 términos si el primero es 0.5?
0.5, 2, 3.5, 5, 6.5, 8, 9.5, 11, 12.5 y 14
2.¿Cuáles son los primeros 10 términos de una sucesión si el inicial es 2/3 y la diferencia entre dos términos consecutivos es 1/6?
2/3, 5/6, 1, 7/6, 4/3, 3/2, 5/3, 11/6, 2 y 13/6
3.El primer término de una sucesión es 1/3 y aumenta constantemente 0.5. ¿Cuáles son los primeros 10 términos de la sucesión?
1/3, 5/6, 4/3, 11/6, 7/3, 17/6, 10/3, 23/6, 13/3 y 29/6
4.La regularidad de esta sucesión consiste en obtener el término siguiente multiplicando por 3 al anterior. Si el primer término es 1.2, ¿cuáles son los primeros 10 términos de la sucesión?
1.2, 3.6, 10.8, 32.4, 97.2, 291.6, 874.8, 2624.4, 7873.2 y 23619.6
5.¿Cuáles son los cinco términos siguientes de la sucesión 1, 3, 6, 10… si la regla para obtenerlos es: un término se obtiene sumando al anterior el número de su posición?
15, 21, 28, 36 y 45
59. Así aumenta
Pág. 116
En parejas, escriban los términos que faltan y la regularidad que presenta cada sucesión.a) 1/16, 5/16, 9/16, 13/16, ___, ___, ___
17/16, 21/16 y 25/16Regularidad: Aumenta en 4/16
b) 1/8, 1/4, 3/8, __ 5/8, __ , __
4/8 = 1/2, 6/8 = 3/4, 7/8Regularidad: Aumenta en 1/8
c) 1/2, 3/4, 1, 1 1/4, 1 1/2, __, __, __
7/4 = 1 3/4, 8/4 = 2, 9/4 = 2 1/4Regularidad: Aumenta en 1/4
d) 0.75, 1.5, 3, __ 12, 24, __, __
6, 48, 96Regularidad: Se duplica el término anterior.
e) 2, 5, 10, 17, __, __, __
26, 37, 50Regularidad: Se suma el siguiente número impar comenzando por 3.
f) 0, 3, 8, 15, 24, __ , __, 63, 80
35, 48Regularidad: Se suma el siguiente número impar comenzando por 3.
60. Partes de una cantidad
Pág. 117
En equipo, resuelvan estos problemas.En un grupo de 36 alumnos, 1/3 del total son menores de 10 años. ¿Cuántos tienen 10 o más años?
24 alumnos.
¿Qué parte del grupo tiene 10 o más años?
2/3 del grupo.
2.En toda la escuela hay 230 estudiantes en total, de los cuales 3/5 son mujeres. ¿Cuántos son hombres?
92 alumnos.
¿Qué parte del total de los estudiantes son hombres?
2/5
3.De los 45 alumnos que hay en un grupo, 9 obtuvieron calificación mayor que 8. ¿Qué parte del grupo obtuvo 8 o menos de calificación?
36 alumnos = 4/5
4.En la zona escolar hay 15 escuelas a las que asisten en total 3 760 alumnos, de los cuales 2 820 tienen más de dos hermanos. ¿Qué parte del total de alumnos tienen dos hermanos o menos?
940 = 25% = 1/4 del total
61. Circuito de carreras
Pág. 118
El dibujo representa un circuito de carreras cuya longitud es de 12 km. Con base en esta información, anota las cantidades que faltan en la tabla.
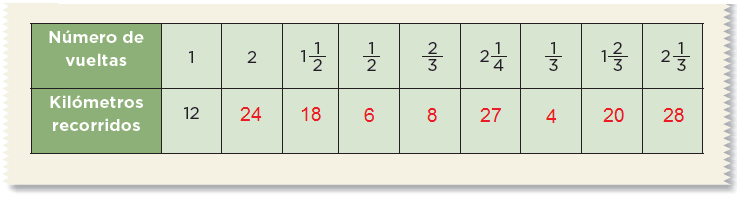
Junto con sus compañeros de equipo, contesten las preguntas con base en la información de la tabla anterior.a) Un ciclista recorrió todo el circuito 3 1/2 veces. ¿Cuántos kilómetros recorrió?
42 kilómetros.
¿Cuántas vueltas completó?
No completó una vuelta, le faltó 1/4 o sea 3 km.
b) Otro ciclista recorrió el circuito 1 1/4 veces. ¿A cuántos kilómetros equivale esa longitud?
15 kilómetros.
c) Un tercer ciclista recorrió 3/4 veces el circuito. ¿Cuántos kilómetros representa esa cantidad?
9 kilómetros.
62. Plan de ahorro
Pág. 120
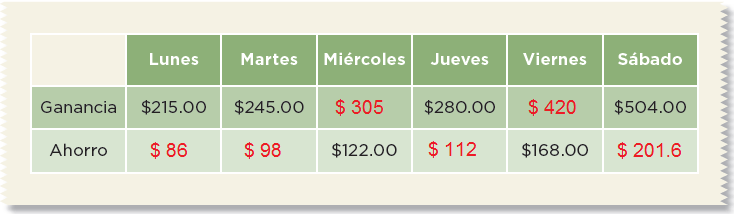
En equipos, resuelvan los problemas.1.Manuel tiene un pequeño negocio y ha decidido ahorrar 2/5 de la ganancia del día. Anota en la tabla las cantidades que faltan.
2.A Yoatzin le gusta correr en el parque Los viveros, en el que hay un circuito de 3 km. de longitud. Primero camina 1/2 de vuelta, luego trota 2/3 de vuelta, después corre 1 1/3 vueltas y para terminar camina 1/6 de vuelta. ¿Cuántos kilómetros recorre Yoatzin en total?
8 km.
3.Calculen los resultados de las siguientes expresiones.a) 3/5 de 256 =
153.60
b) 3/8 de 824 =
309
c) 4/5 de 90 =
72
d) 2/3 x 24 =
16
e) 3/4 x 56 =
42
f) 2 1/2 veces 15 =
37.5
63. Cuerpos idénticos
Pág. 121
En equipos, hagan la siguiente actividad.Armen con cartulina un cuerpo geométrico idéntico al modelo que les proporcionará su profesor; deberá tener la misma forma y tamaño, pero no pueden desarmar el modelo para copiarlo.
Es necesario que realices la actividad en tu salón de clases con tus compañeros y la guía de tu maestro.
64. El cuerpo oculto
Pág. 122
Organicen equipos para realizar esta actividad.El profesor distribuirá a cada equipo un cuerpo geométrico cubierto o dentro de algo; eviten que los demás equipos lo vean.
Es necesario que realices la actividad en tu salón de clases con tus compañeros y la guía de tu maestro.
65. ¿Cuál es el bueno?
Pág. 123
En parejas. lleven a cabo las siguientes actividades.1.Seleccionen y encierren los desarrollos planos con los que se puede armar cada cuerpo geométrico.
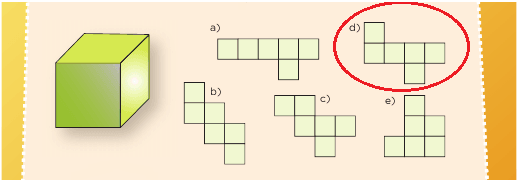
1.Seleccionen y encierren los desarrollos planos con los que se puede armar cada cuerpo geométrico.
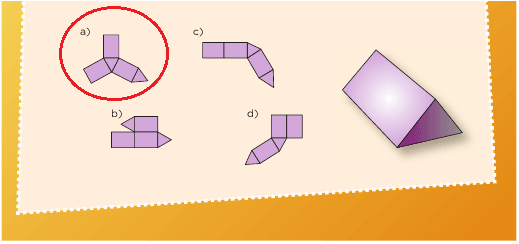
2.Copien las siguientes figuras en su cuaderno y dibujen las caras necesarias para completar el desarrollo plano con el que se pueda construir cada cuerpo geométrico que se menciona.
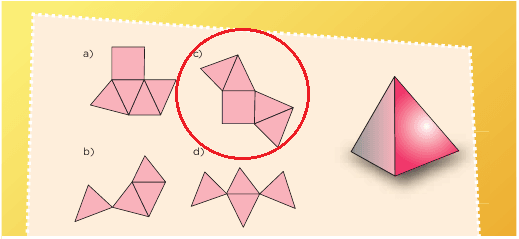
66. ¿Conoces a π?
Pág. 125
En equipos, lleven a cabo la actividad y después contesten lo que se pide.Utilicen hilo de cuerda para medir la circunferencia y el diámetro de los objetos que tienen en su mesa y registren sus resultados en la tabla. Después obtengan sus cocientes y completen la tabla; pueden usar calculadora. Escriban sólo dos cifras decimales para expresar el cociente.
Las respuestas de la tabla dependen en su totalidad de las medidas de los objetos que sean proporcionados por tu maestro en el salón de clases.
a) ¿Cómo son los resultados de los cocientes?
Todos son equivalentes a un poco más de 3.
¿A qué crees que se deba esto?
A que es un valor constante que descubrieron los matemáticos y que es equivalente a 3.1415…. y que normalmente está redondeado a 3.1416; se representa con la letra griega π (pi).
b) ¿Cómo calcularían la medida de la circunferencia si conocen la medida del diámetro?
Es necesario multiplicar el diámetro de la circunferencia por π, cuyo valor equivale a 3.1416
67. ¿Para qué sirve π?
Pág. 126
En equipos, resuelvan los siguientes problemas; pueden usar calculadora.1.Si el diámetro de la Tierra es de 12 756 km, ¿cuál es la medida de su circunferencia?
40 074.2496 km. (tomando al π con valor de 3.1416, ya que en ocasiones se utiliza el valor de 3.14)
2.Si la medida de la circunferencia de una glorieta es de 70 m., ¿cuánto mide su diámetro?
22.2816399 m.
3.De la casa de Pancho a la de José hay una distancia de 450 m. Si vas en una bicicleta, cuyas ruedas tienen un diámetro de 41.5 cm., ¿cuántas vueltas darán éstas en el trayecto de la casa de Pancho a la de José?
345.154491 vueltas por cada llanta. 690.308982 por las dos llantas.
69. ¿Qué pasa con el volumen?
Pág. 128
En parejas. consideren los siguientes prismas para responder las preguntas. Tomen en cuanta que un obstáculo impide ver parte de los prismasa) ¿Cuál podría tener un volumen equivalente a 18 cubos?
El prisma morado.
b) Si la altura de ambos equivale a 4 cubos, ¿cuál es la diferencia entre sus volúmenes?
8 unidades cúbicas.
c) Si duplican el número de cubos a lo ancho de cada cuerpo, ¿En cuánto se incrementa su volumen?
El volumen se duplica.
d) Si duplican el número de cubos tanto a lo largo como a lo ancho, ¿en cuánto aumenta su volumen?
El volumen aumenta cuatro veces.
70. Cajas para regalo
Pág. 129
En parejas, resuelvan los siguientes problemas.1. Anita compró 30 chocolates que tienen forma cúbica, cuyas aristas miden 1 cm. Desea empacarlos como regalo en una caja que tenga forma de prisma rectangular.a) ¿Cuáles deben ser las medidas de la caja, de manera que al empacar los chocolates no falte ni sobre lugar para uno más?
15 x 2 x 1 cm., 10 x 3 x 1 cm. o 5 x 3 x 2 cm.
b) ¿Es posible empacar tal cantidad de chocolates en una caja de forma cúbica, sin que sobre o falte espacio para uno más?
No.
Si la respuesta es sí, ¿cuáles tendrían que ser las medidas de la caja?
Tres números iguales que multiplicados por sí mismos nos den 30.
Si la respuesta es no, ¿por qué?
Por que no existen tres números enteros iguales que al multiplicarse por sí mismos, den como resultado 30.
2.¿Cuál es el volumen, en cubos, del prisma triangular que está a la derecha?
37.5 unidades cúbicas.
71. ¿Qué música prefieres?
Pág. 130
En equipos, resuelvan los siguientes problemas.1.A los alumnos de los grupos de sexto grado de una escuela primaria se les aplicó una encuesta sobre el tipo de música que prefieren. La música de banda fue de las más elegidas; en el grupo A, la seleccionaron 1 de cada 2 alumnos; en el B, 3 de cada 4; y en el C, 7 de cada 10. ¿Qué grupo tiene mayor preferencia por este género de música?
En el grupo B.
2.Con la misma encuesta, en los grupos de quinto grado se obtuvieron los siguientes resultados: en el grupo A, 50% de los estudiantes eligieron el hip hop y una cuarta parte la música de banda. En el B, 2 de cada 5 niños prefirieron la música grupera y 1 de cada 2 eligió el hip hop. ¿En qué grupo hay mayor preferencia por el hip hop?
En ambos grupos la preferencia por el hip hop es la misma.
¿Qué tipo de música, grupera o de banda, gusta más entre los alumnos de quinto grado?
La música grupera.
73. Los medicamentos
Pág. 134
En equipos, resuelvan el siguiente problema.La señora Clara visitó al médico porque padecía una infección en la garganta. El tratamiento que le recetó consta de varios medicamentos, según se explica en la tabla:Completen la siguiente tabla en donde se registra el tiempo transcurrido a partir del inicio del tratamiento; consideren que la primera toma de los tres medicamentos la hace al mismo tiempo.
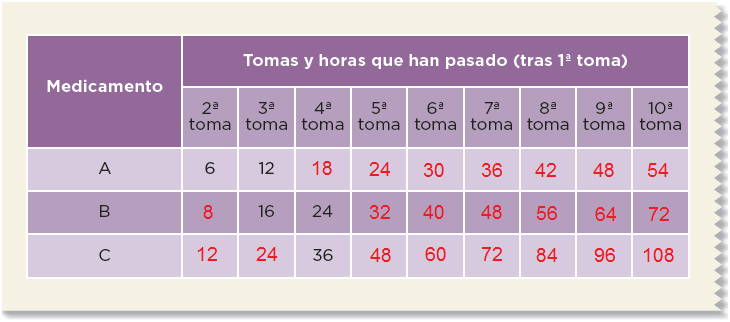
1.Después de la primera toma, ¿cuántas horas deben transcurrir para que ocurra otra toma simultánea de al menos dos medicamentos?
12 horas.
2.Al cumplir tres días con el tratamiento, ¿cuántas veces ha coincidido la toma simultánea de los tres medicamentos?
3 veces.
3.Si el viernes a las 8:00 de la mañana la señora Clara comenzó a ingerir los tres medicamentos, ¿cuáles deberá tomar el domingo a las 12 horas?
No deberá tomar ningún medicamento.
Individualmente, resuelve los siguientes problemas.1.Encuentra los primeros 10 múltiplos comunes de 7 y 10.
70, 140, 210, 280, 350, 420, 490, 560, 630 y 700.
2.Encuentra el décimo múltiplo común de 5 y 9.
450
3.Encuentra todos los números que tienen como múltiplo común el 20.
2, 4, 5 y 10.
74. Sin cortes
Pág. 136
En equipos, resuelvan los siguientes problemas.1.Se quiere cubrir un piso rectangular de 450 cm. de largo y 360 cm. de ancho con losetas cuadradas de igual medida. No se vale hacer cortes, es decir, el número de losetas tendrá que ser un número entero.a) Escriban tres medidas que pueden tener las losetas para cubrir todo el piso.
Losetas de 30, 45 y 90 cm. por lado.
b) ¿Cuál es la medida mayor?
Loseta de 90 cm. por lado.
2.En la ferretería tienen dos tambos de 200 litros de capacidad. Uno contiene 150 litros de alcohol y el otro 180 litros de aguarrás. Se decidió mandar hacer varios garrafones del mismo tamaño y capacidad para envasar tanto el alcohol como el aguarrás sin que sobre nada de líquido en los tambos.a) ¿Es posible que la capacidad de los garrafones sea de entre 10 y 20 litros?
Sí.
¿Por qué?
Porque entre 10 y el 20 encontramos los siguientes divisores comunes de 180 y 150: 10 y 15.
b) Escriban tres capacidades diferentes que pueden tener los garrafones.
10, 15 y 30.
Antes de ordenar la fabricación de los garrafones, llegó a la ferretería un tercer tambo con 105 litros de cloro. Ahora se necesita que los tres líquidos sean envasados en garrafones con el mimo tamaño y capacidad.c) Escriban dos capacidades diferentes que pueden tener los garrafones.
3, 5 y 15 litros.
d) ¿Cuál será el de mayor capacidad?
15 litros.
Individualmente, resuelve lo siguiente.1.¿Cuáles son los divisores comunes de 3, 9 y 12?
1 y 3
2.¿Qué divisores tienen en común 20, 32 y 60?
1, 2 y 4
3.Escribe los divisores comunes de 90 y 70.
1, 2, 5 y 10
75. Paquetes escolares
Pág. 139
En equipos, resuelvan los siguientes problemas.1.Al hacer paquetes de 6 libretas y paquetes de 6 lápices de colores, los maestros de una escuela se percataron de que había más paquetes de lápices que de libretas, y de que en ambos casos no sobraba nada. Se sabe que la cantidad original de libretas está entre 185 y 190, y la de lápices, entre 220 y 225. ¿Cuál será la cantidad original de libretas y lápices de colores?
186 libretas y 222 lápices.
2.Lean y discutan las siguientes afirmaciones. Concluyan si son verdaderas o falsas y expliquen su decisión.
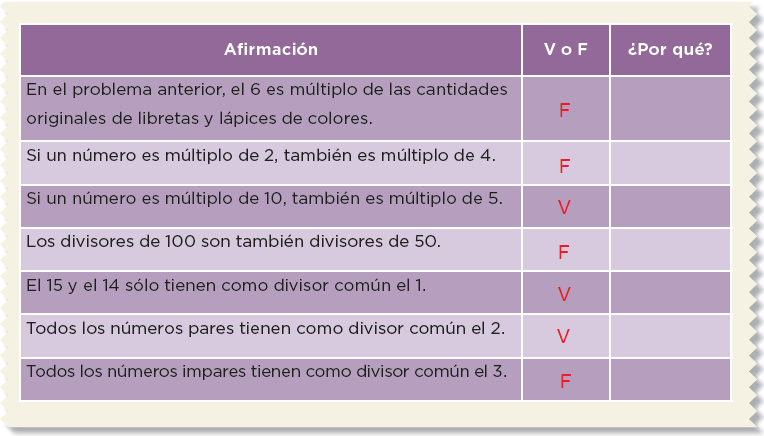
76. Estructuras secuenciadas
Pág. 140
En pareja, resuelvan los problemas.1.Las siguientes estructuras están armadas con tubos metálicos y hojas cuadradas de vidrio.a) ¿Cuántos tubos metálicos se necesitan para hacer la estructura 4?
13 tubos metálicos.
b) ¿Cuántos tubos metálicos se necesitan para hacer una estructura con 10 hojas de vidrio?
31 tubos metálicos.
c) ¿Y con 15 hojas de vidrio?
46 tubos metálicos.
2.Estas estructuras están armadas con tubos metálicos y hojas pentagonales de vidrio.a) ¿Cuál es la sucesión numérica que representa las cantidades de tubos de las estructuras?
5, 13, 21 y 29.
b) ¿Cuántos tubos y cuántas hojas de vidrio se necesitan para formar la estructura 10?
77 tubos y 19 vidrios.
c) ¿Y para la estructura 15?
117 tubos y 29 vidrios.
77. Incrementos rápidos
Pág. 142
En equipos, resuelvan los siguientes problemas.1.Con base en las siguientes figuras contesten lo que se pide. Consideren como unidad de medida un cuadro.a) ¿Cuál es la sucesión numérica que representa las áreas de los triángulos?
Sucesión: 0.5, 2, 8 y 32
b) ¿Cuál será el área de los triángulos en las figuras 6, 7 y 8?
512, 2 048 y 8 192
2.Consideren el número de lados de las figuras para completar la sucesión que representa el número de lados de las primeras 5 figuras.
Sucesión: 3, 12, 48, 192 y 768
3.Las siguientes figuras representan una sucesión de cuadrados.a) Escriban la sucesión numérica que representa las primeras 10 medidas de los lados cuadrados.
Sucesión: 3, 6, 12, 24, 48, 96, 192, 384, 768 y 1 536
b) La siguiente sucesión corresponde a las áreas de las regiones sombreadas de los cuadrados. ¿Cuáles son los términos que faltan?
Sucesión: 4.5, 18, 72, 288, 1 152, 4 608 y 18 432
78. Números figurados
Pág. 144
En pareja. Escriban los dos términos numéricos que continúan cada sucesión. Triangulares:
15 y 21
Escriban los dos términos numéricos que continúan cada sucesión. Cuadrangulares:
25 y 36
Escriban los dos términos numéricos que continúan cada sucesión. Pentagonales:
35 y 51
Escriban los dos términos numéricos que continúan cada sucesión. Hexagonales:
45 y 66
79. Para dividir en partes
Pág. 145
En equipos, resuelvan los siguientes problemas.1.De un grupo de alumnos, 4/6 van a participar en un concurso de danza. La mitad de ellos presentará una danza folclórica y la otra mitad, una pieza de danza clásica. ¿Qué parte del total de alumnos participará en cada una de las dos piezas de danza?
2/6 = 1/3 (un tercio) de los alumnos.
2.Al trasladar una pieza de madera se daño una quinta parte. Con el resto de la madera en buen estado se van a construir 2 puertas de igual tamaño. ¿Qué parte de la pieza original se utilizará en cada una de las puertas?
2/5 de la pieza original
3.En la ferretería La Tía Adriana, vaciaron 6/7 de una lata de pintura en 3 recipientes iguales, la misma cantidad en cada uno. ¿Qué parte de la lata de pintura se vació en cada recipiente?
2/7 de lata de pintura
80. Repartos equitativos
Pág. 146
En equipos, resuelvan los siguientes problemas.1.Cuando Raúl y Esperanza llegaron a una fiesta quedaban 3/10 del pastel, así que se dividieron esa porción en partes iguales. ¿Qué parte del pastel completo le tocó a cada uno?
3/20 del pastel original.
2.Cuatro amigos van a repartirse, por partes iguales y sin que sobre nada, 5/8 de una pizza. ¿Qué parte del total, es decir, de la pizza completa, le tocará a cada uno?
5/32 de la pizza.
3.Patricia tiene 3/4 m de listón y lo va a cortar para hacer 4 moños iguales. ¿Qué cantidad de listón ocupará para cada moño?
3/16 de listón.
81. ¿Cuánto cuesta un jabón?
Pág. 147
En equipos, resuelvan este problema.En el almacén La Abarrotera pusieron en oferta paquetes de jabón para tocador. De acuerdo con la información de la tabla, ¿cuál es la oferta que más conviene?
La marca Fresquecito.
Individualmente, resuelve las siguientes operaciones.a) 10.5 ÷ 4 =
2.625
b) 350.45 ÷ 8 =
43.80625
c) 258.9 ÷ 10 =
25.89
d) 57 689.6 ÷ 100 =
576.896
e) 674 567 ÷ 1 000 =
674.567
82. Transformación de figuras
Pág. 149
En parejas, hagan lo que se indica a continuación.Recorten los rombos de la página 157 y calculen su perímetro y área.En uno de los rombos, uno de ustedes recorte sobre la diagonal mayor y forme la figura 1.Sobre el otro rombo, el otro compañero debe recortar sobre la diagonal menor y formar la figura 2.Cada uno calcule el perímetro y el área de la nueva figura que obtuvo,Finalmente, entre los dos respondan las preguntas.a) Al recortar el rombo sobre una de sus diagonales, ¿cómo son los dos triángulos que se obtienen?
Son iguales.
b) ¿Qué sucedió con el perímetro del rombo con respecto al perímertro de la nueva figura?
Cambia según la diagonal por la cual se divide.
c) ¿Qué sucedió con el área del rombo con respecto al área de la nueva figura?
El área del rombo se mantiene.
83. Juego con el tangram
Pág. 150
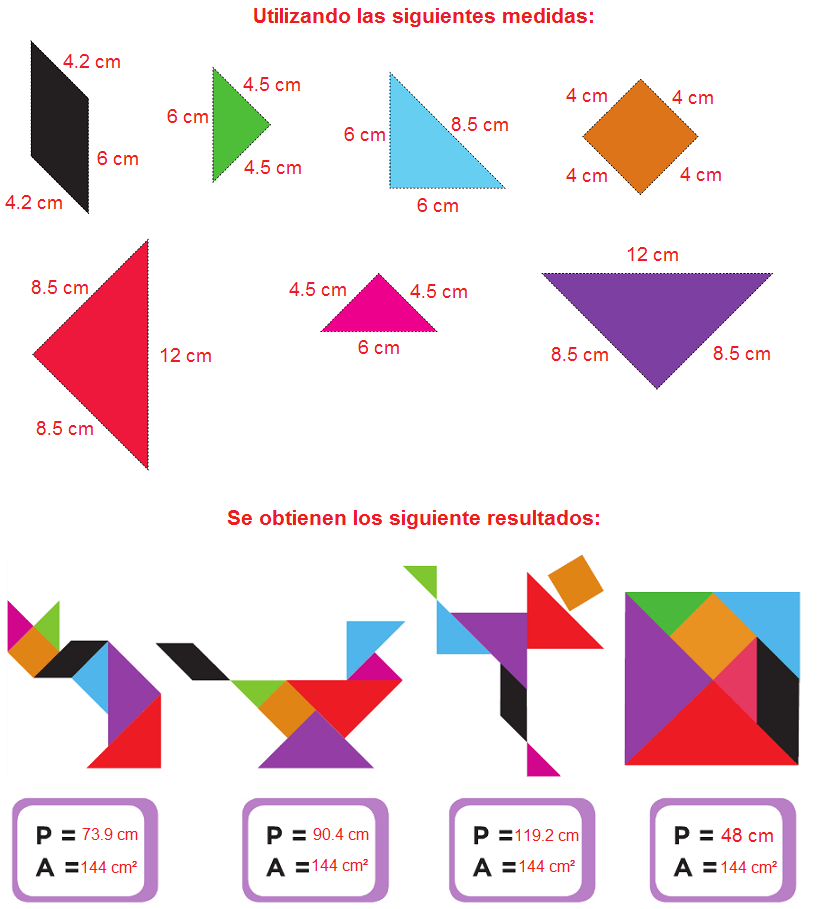
En parejas, recorten las piezas del tangram de la página 155, reproduzcan las figuras que se muestran abajo y calculen su perímetro y área.
85. Hablemos de nutrición
Pág. 152
En equipos, resuelvan los siguientes problemas con base en los datos de la tabla. Si lo consideran necesario pueden usar su calculadora.1.Si comparamos el arroz, los frijoles y las tortillas, ¿cuál alimento es el más rico en carbohidratos?
El arroz.
2.Si consideramos el huevo, la carne de res y el pescado, ¿cuál alimento es el más rico en proteínas?
El pescado.
3.¿Cuál es el alimento más rico en lípidos?
La carne de res y el huevo.



