¿Buscas las respuestas a todas las preguntas de desafíos matemáticos 4 grado? Estas en la página ideal! Descubre las soluciones del libro de matemáticas 4 grado.
Puedes seguir haciendo scroll y encontrar las soluciones o pulsar ctrl + f (cmd + f en mac) en tu ordenador para buscar la respuesta a una pregunta que te han puesto como tarea. Te recomendamos que antes de mirar la respuesta intentes buscarla por ti mismo/a y que utilices esta página para comprobar si es correcta. Recuerda, las matemáticas también pueden ser divertidas y completar estos libro de matemáticas 4 grado contestado te ayudaran a desarrollar la lógica.
Puedes descargar el PDF AQUÍ o consultar Ecuaciones, Desafíos Matemáticos quinto grado, Desafíos Matemáticos sexto grado
2. Suma de productos
Pág. 13
1. En el estante de una ferreteria…¿Cuántos tornillos hay en el estante?
6 610 tornillos
2. Fernando lleva en su camión…¿ Cuántas naranjas lleva en total?
4 573 naranjas en total
3. Un estadio de futbol cuenta con..¿Cuál es la capacidad total del estadio?
6 610 asientos en total
4. La cajera de una tienda…¿ Cuánto dinero entregó en total?
$ 4 573 Pesos
5. Ayer jugamos boliche…¿ Cuántos puntos conseguí?
6 610 Puntos
6. A la dulcería llegó este pedido… ¿Cuántas golosinas incluía el pedido?
4 573 Golosinas
Identifica las operaciones correspondientes a los ejercicios anteriores:

3. ¡Lo tengo!
Pág. 15
Juega con tres compañeros
Realizar la actividad en físico
4. Décimos, centésimos y milésimos
Pág. 16
a) ¿Cuántos décimos caben en una unidad?,¿cuántos centésimos caben en un décimo?…
10 décimos caben en 1 unidad 10 centésimos caben en 1 décimo 10 milésimos caben en 1 centésimo
, decimales y equivalencias
b) ¿Qué es más grande, un décimo o un centésimo?
Un décimo
, decimales y equivalencias
c) ¿Cuántos milésimos caben en un décimo?
100 milésimos en un décimo
, decimales y equivalencias
d) ¿Cuántos milésimos caben en una unidad?
En una unidad caben 1000 milésimos
, decimales y equivalencias
e) En dos décimos, ¿cuántos centésimos hay?
2 decimos es igual a 20 centésimos
Puedes escribirlo en unidades así: 0.20
, decimales y equivalencias
f) ¿Cuántos décimos hay en media unidad?
5 decimos en una unidad
, decimales y equivalencias
g) ¿Cuántos décimos hay en 1 unidad + 5/10?
15/10
, decimales y equivalencias
h) ¿Cuántos milésimos tienen 1.5 unidades?
1500 milésimos
, decimales y equivalencias
5. Expresiones con punto
Pág. 18
En parejas…
Realizar la actividad en físico. Algunas observaciones a considerar al momento de realizar la actividad es muy importante que realices la actividad de la página 16, ya que con este material medirás todas las cosas que se piden.
6. La fábrica de tapetes
Pág. 19
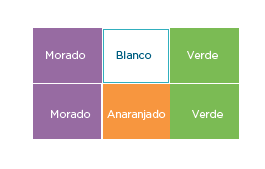
a)¿Qué fracción representa la superficie de color anaranjado?
1/6
b) ¿Qué fracción representa la superficie morada?
1/3
c) ¿Qué colores juntos cubren la mitad del tapete?
Morado y blanco, como también naranja y verde.
1. Queremos un tapete cuadrangular que tenga cuatro colores
7. Fiesta y pizzas
Pág. 20
¿Qué porción de pizza le tocó a cada integrante de cada grupo?
Grupo 1 (porción por persona) : 2/3 de pizzaGrupo 2 (porción por persona) : 1 1/3 de pizzaGrupo 3 (porción por persona) : 3/5 de pizzaGrupo 4 (porción por persona) : 3/4 de pizza
¿En qué grupo le tocó menos pizza a cada persona?
En el grupo 3
Representen las pizzas que se necesitan para que en un grupo de 6 personas a cada una le toque 4/6

8. Y ahora, ¿cómo va?
Pág. 22
1. Encuentra los elementos faltantes en las siguientes sucesiones.
Sucesiones
a) Encierra en un círculo las figuras que forman parte de la sucesión anterior…
Sucesiones
a) Encierra en un círculo las figuras que forman parte de la sucesión anterior
Sucesiones
2. ¿Qué elementos faltan en esta sucesión? Dibújalos sobre las líneas.
Respuesta de las dos siguientes figuras :
Sucesiones
a) Estas figuras forman parte de la sucesión anterior; anota qué lugar ocupan.
Sucesiones
9. ¿Cuáles faltan?
Pág. 24
Encuentren los elementos faltantes en las siguientes sucesiones y contesten las preguntas.
3, 5, 8, 8, 13, 11, 18, 14 , 23, 17, 28, 20, 33, 23, 38, 26, 43, 29 , 48 , 32, 53, 35 , 58, 38, 63, 41, 68, 44,73 , 47…
Sucesiones
a) ¿Qué números deben ir en los lugares 40 y 41?
62 y 103
Sucesiones
b) ¿Qué regla se establece en la sucesión anterior? Escríbanla con sus propias palabras:
Ejemplo:al 3 del inicio se le suman 5 unidades y posteriormente 3 unidades, por otra parte al 5 del inicio se le suman 3 unidades al principio y posteriormente 5 unidades.
Sucesiones
Resolver la siguiente sucesion…
300,5 300, 600,5 250, 900, 5 200, 1200, 5 150, 1500,5100, 1 800,5050, 2100, 5000 …
Sucesiones
a) De la sucesión anterior, ¿qué número corresponderá al lugar 20?
4,850
Sucesiones
b) ¿Hay algún número que se repita en esa sucesión?
Algunos que se repiten 4500 , 4800 y 5100
Sucesiones
c) De los números que van disminuyendo, ¿alguno podrá ocupar el lugar 31?
No
Sucesiones
d) Escriban la regla que se establece en esa sucesión.
En esta sucesión a los números nones se les suma 300 unidades, mientras que a los pares se les resta 50 unidades.
Sucesiones
10. La tienda de doña Lucha
Pág. 26
Juan compró una torta de pollo y un jugo…¿quien de los dos dos pagó más?
Raúl
2. Anoten los alimentos que puede haber en las bolsas de Jessica y de Rogelio:
Jessica1 Torta de chorizo1 Licuado
Rogelio1 Torta especial1 Jugo
1. Paula registró en una libreta sus ahorros…¿Cuánto ahorró en total?
$ 125.15 pesos
2. Resuelvan los ejercicios:
a) 35.90 + 5.60 = 41.50b) 89.68 + 15.60 = 105.28c) 145.78 + 84.90 + 19.45 = 250.13
11. Los uniformes escolares
Pág. 28
a) Si la mamá de Juan tiene $1 000.00, ¿le sobra o le falta dinero para comprar esas prendas?
Le sobra $149.2 pesos
1. Con un billete de $20.00 se pagó una cuenta de $12.60. ¿Cuánto se recibió de cambio?
$ 7.4 pesos
2.Paulina necesita un pincel que cuesta $37.50…¿Cuál es la diferencia entre los dos precios?
$ 7.6 pesos
3. La mamá de Perla fue al mercado…¿Cuánto le dieron de cambio si pagó con un billete de $100.00?
$ 23.9
4. Agustín tenía cierta cantidad de dinero ahorrado… ¿Cuánto tenía ahorrado?
$ 47.5
5. 35.60 – 5.90 =
$ 29.70
6. 79.95 – 25.60 =
$ 54.35
7. 184.90 – 59.45 =
$ 125.45
12. Butacas y naranjas
Pág. 30
¿Alcanzarán las butacas del teatro …
Si
2. una bodega de la central de abastos distribuye… preguntas a) y b)
a) Mercado morelosb) 708 naranjas
13. Combinaciones
Pág. 31
1. ¿Cuántas casas diferentes entre sí, pero similares a las del modelo…
12 casas diferentes
2.¿Cuántos postres diferentes se pueden servir?
8 postres
3.¿Cuántas parejas de baile diferentes se podrán formar con los invitados?
270 parejas
14. ¿Alcanza?
Pág. 32
1. Una pieza de tela mide 15 m de largo por 1.5 m de ancho. ¿Cuánto mide la superificie de la tela?
22.5 m
2. Un terreno de forma rectangular mide 210m2 de superficie y el ancho mide 7m.¿Cuánto mide de largo?
En este problema tienes que calcular el largo de la figura, la informacion que te dan es 210 m² de superficie (área) y un ancho de 7 m, la unidad de medida que maneja es en metros. Para calcular vamos a realizar una división 210 entre 7 210 / 7 = 30 m
para comprobar si es correcto podemos realizar la multiplicación 30 m x 7 m = 210 m², el total del área se representa en metros cuadrados.
3. Samuel tiene 11 cajas con mosaicos… ¿será necesario que compre más cajas?
No.Por que requiere de 150 mosaicos y compró 154.
15. ¿Cómo se ven?
Pág. 33
1. Un vaso visto desde abajo y de frente, a la altura de tus ojos.
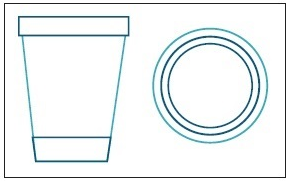
2. Un escritorio visto desde arriba y desde un lado.
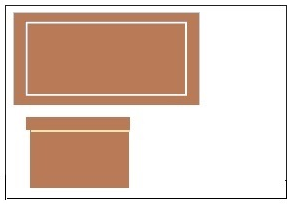
3. La siguiente pila de cajas vista desde arriba y desde el lado derecho.
a) 12 cajasb) 8 cajas
16. Diferentes vistas
Pág. 34
En equipos de tres, lleven a cabo las actividades sentados en el piso.
Ejemplo de respuesta.
17. ¿Equiláteros o isósceles?
Pág. 35
En equipos, tengan listos los triángulos de su material recortable, p. 249,
escalenos (5, 7 ,10, 12, 14)
isósceles (2, 3, 4, 9, 15)
a) ¿Cómo describirían un triángulo isósceles?
ejemplo de respuesta: Es aquel que tiene dos lados iguales.
¿Y un escaleno?
Un triángulo escaleno tiene sus tres lados diferentes.
b) ¿Hay triángulos que sean isósceles y equiláteros al mismo tiempo?¿Por qué?
Sí.Todo triángulo equilátero es un triángulo isósceles, pero no todo isósceles es equilátero.
18. ¿Un triángulo que es rectángulo?
Pág. 37
Averigüen entre los triángulos que usaron en la clase anterior cuáles tienen un ángulo recto..
2, 7, 10 y 14
1.¿Existen triángulos escalenos con un ángulo recto?
Sí
2. ¿Todos los triángulos escalenos tienen un ángulo recto?
No
3. Indiquen un triángulo isósceles que tenga un ángulo recto.
El triangulo número 2
4. ¿Hay triángulos equiláteros con un ángulo recto?
No hay
19. ¡Adivina cuál es!
Pág. 38
En equipos, participen en el juego “¡Adivina cuál es!”.
En este ejecicio se trabaja en equipo con apoyo de su maestro y su material recortable de las páginas que se indican.
20. ¿Hicimos lo mismo?
Pág. 39
En equipos, formen cuadriláteros con el material (triángulos) que utilizaron en la clase anterior.
Con los triángulos deben formar cuadriláteros al unir algunos de sus lados.Gana el equipo que más cuadriláteros diferentes haya formado.
21. Al compás del reloj
Pág. 40
1. ¿A qué horas deberá tomar la segunda y la tercera pastilla?
Segunda pastilla a las 2:30 p.mTercer pastilla a las 8:30 p.m.
2. ¿A qué hora se llegará a Veracruz si el viaje se inicia a las 9:50 horas?
15: 10 o lo que es los mismo las 3:10 p.m.
3. ¿A qué hora salí de mi casa?
A las 11:45 a.m.
En parejas, expresen de diferentes formas la hora que marca cada reloj.

22. El tiempo pasa
Pág. 42
1. ¿Cuándo hizo el primer pago?
5 de Noviembre
2. ¿Cuándo inicia su periodo de descanso? ¿Cuándo tiene que presentarse en la plataforma?
22 de Julio y regresa el 5 de Agosto.
3. ¿en qué periodos le tocará participar? ¿Todos los equipos participarán el mismo número de veces?
5 ta y 11 va semana .No, a los primeros equipos les tocara más veces que a los ultimos.
4. ¿en qué fechas iniciarán las tres estaciones restantes?
20 de Junio, 20 de Septiembre y 20 de Diciembre.
23. Piso laminado de madera
Pág. 43
a) ¿Cuánto cuestan tres cajas de piso laminado de 6 mm de grosor con descuento?
$ 2,160
b) ¿Cuántas cajas de piso laminado de 6 mm se deben comprar para cubrir un piso de 14 m2?
4 cajas
c)¿Cuál es el costo total del material necesario de piso laminado de 7 mm…
$ 2, 640 con descuento 2,380
a) ¿Cuál es la capacidad de la botella que corresponde a esta etiqueta?
1.5 Lts.
b) ¿Cuántos mg de sodio contiene la botella de agua que corresponde a esta etiqueta?
75 mg
c) ¿A qué cantidad de agua corresponde la información nutrimental de la etiqueta?
100 ml
25. ¿Cuál es la escala?
Pág. 48
En equipos, localicen en cada recta los números que se indican: El número 5
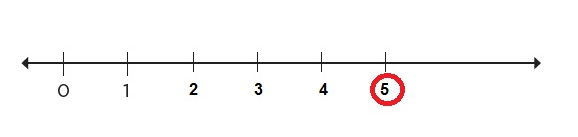
El número 10
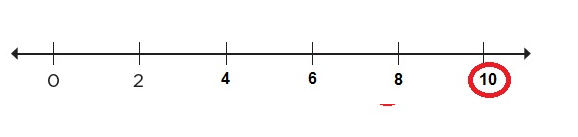
Los números 4 y 20
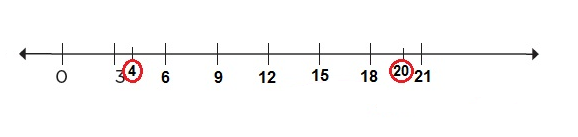
26. ¿Es necesario el cero?
Pág. 49
Los números 2 y 9

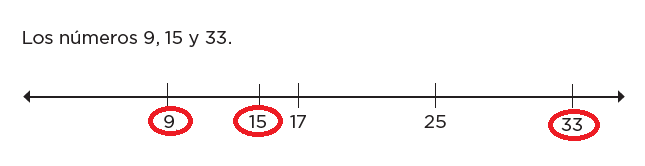
Los números 9, 15 y 33
Los números 26 y 41

27. Cero información
Pág. 50
Los números 20, 50 y 80

Los números 300, 500 y 750

Los números 175, 250, 300 y 475

28. ¿Qué fracción es?
Pág. 51
1. ¿Qué fracción representa la parte pintada de cada i gura? Escriban la respuesta debajo de la figura.
Primer figura (rectángulo) 1/2segunda figura(círculo) 2/5Tercer figura (triángulo) 2/3Cuarta figura (cuadrado) 1/4
equivalentes
2. De las siguientes figuras, ¿en cuál está pintada la mitad?, ¿la tercera parte? y ¿la cuarta parte? Comenten.
A. cuarta parteB. tercera parteC. mitadD. cuarta parteE. mitad
equivalentes
3. Indiquen qué fracción representa cada sección del cuadrado, y escriban la respuesta en cada una.
Parte naranja bajo 1/4Parte naranja fuerte 1/8Parte café 3/8Parte morada 1/4
equivalentes
4. Si cada rectángulo se considera una unidad, ¿qué fracción representa la parte pintada? Escriban en el recuadro.
equivalentes
5. Si el segmento mayor se considera una unidad, indiquen la fracción que representa cada uno de los segmentos menores.
a) 1/6b) 1/4c) 1/2d) 4/6 = 2/3 (simplificando fracciones)
equivalentes
29. Partes de un todo
Pág. 53
1. En cada figura iluminen la fracción que se indica:
equivalentes
2. En cada figura representen la fracción que se indica:
equivalentes
3. Utilicen figuras para representar las fracciones 2/3 y 8/5 :
Ejemplo de respuesta equivalentes
4. Consideren que el segmento representa la unidad y tracen otros segmentos con estas longitudes:
equivalentes
1. 2/4 de color verde, 1/8 de anaranjado y 1/16 de amarillo. Ningún triángulo puede iluminarse dos veces.
¿Cuántos triángulos pequeños se iluminaron? 22
equivalentes
2. 2/5 de rojo y 1/3 de rosa. Cuida que no se sobrepongan ambas zonas
¿Cuántos rectángulos quedaron sin iluminar? 16
30. En busca del entero
Pág. 56
1. El segmento representa 1/5 de la unidad; tracen la unidad.
equivalentes
2. El triángulo representa 2/6 de una figura; dibujen la figura completa.
equivalentes
3. El rectángulo representa 2/3 de un entero; dibujen el entero.
equivalentes
31. El más rápido
Pág. 57
Actividad
Actividad para realizar en equipo, según las indicaciones de su maestro
32. Tarjetas decimales
Pág. 58
Actividad
El profesor les indicara los detalles del juego.En equipos, nombren a un “juez o árbitro” en cada equipo y jueguen lo siguiente con el material recortable, pp. 239 y 241.Para cada equipo: 30 tarjetas con números decimales
33. Figuras para decorar
Pág. 59
En equipos, anoten después de cada decorado cuál o cuáles cuerpos se usaron para hacerlo y justii quen su respuesta.
la tercer diseño c), b) o d)
el cuarto diseño d)
Expliquen qué cuerpos utilizarían para hacer la siguiente figura
Figura c)La figura del hexágono, si pueden observar se puede dividir en 6 triangulos iguales.
34. Como gran artista
Pág. 62
Actividad
Actividad para realizar en clase utilizando su juego de geometría.
36. El transportador
Pág. 64
Construye un transportador siguiendo los pasos que se muestran.
Realizar la actividad con su juego de geometría.
a) ¿Qué fracción del círculo es cada una de las partes en que quedó dividido?
1/12
b) Además de los ángulos de 90°, ¿cuántos grados mide cada fracción del círculo?
30°
c) ¿Cuántos doceavos del círculo abarca un ángulo de 150°?
5
d) Si doblas a la mitad cada doceavo obtenido, ¿qué medida de ángulo resulta?
15º
38. Uso del transportador
Pág. 67
En equipos, hagan los ejercicios y comenten lo que se pide
A. 120ºB. 210ºC. 45ºD. 60ºE. 285ºF. 150º Y 30º
Con el transportador que construyeron, tracen en su cuaderno ángulos de igual medida que los que aparecen a continuación.
Mediante el uso de tu transportador primero debes medir los ángulos y luego trazarlos, puedes seguir el siguiente método:Para medir ángulosPrimero debes posicionar el centro del transportador en el vértice del ángulo y la línea en el cero grados:Una vez ubicado el centro del transportador en el vértice del ángulo, y en cero grados. Vamos a medir el ángulo, siguiendo la numeración en contra de las manecillas del reloj:Si necesitas medir otros ángulos que no precisamente estén posicionados de manera horizontal, lo que debes hacer es siempre colocar el centro del transportador en el vértice del ángulo, asegurándote de que la base del ángulo este también alineada con el cero grados.
Para trazar ángulos
Primero debes trazar una línea horizontal, que servirá para indicarnos 0° grados.Luego, coloca el centro del transportador en el extremo izquierdo de la línea, es decir en el punto con la letra “a”.Una vez puesto el centro del trasportador sobre el origen de la línea, y el cero grados ubicado también sobre la línea; vamos a buscar la medida del ángulo que queremos trazar, en contra de las manecillas del reloj y ponemos una marca.Y finalmente trazamos una línea del origen “a” de la línea, hacia la marca que hicimos. De esa forma obtenemos el ángulo con la medida que estábamos buscando.
Nota
Esta página se resuelve con la experiencia de cada alumno.
39. Pequeños giros
Pág. 69
a) ¿Cuántos grados mide el ángulo que forman las líneas rojas?
a) 90º
b) ¿Qué fracción de un giro completo representa?
1/4
c) ¿Cuántos grados mide cada uno de los tres ángulos que se formaron con los dobleces en el punto 2?
30º
d) ¿Y cuántos grados medirán los ángulos marcados con líneas verdes?
10º
e)¿Qué pasa si haces lo mismo en un círculo más pequeño o en un círculo más grande, se conservarán las medidas anteriores?
se conservan las medidas
f) ¿Todos los equipos obtuvieron las mismas respuestas? ¿A qué crees que se deba?
respuesta que deben dar los alumnos con su propio criterio.
a) ¿Cuánto mide cada ángulo de los que acabas de trazar?
1º
b) ¿Cuántos grados mide el cuarto de círculo que tiene cada uno de ustedes?
90º
c) Los cuatro integrantes del equipo junten su cuarto de círculo de manera que coincidan
360º
40. Dale vueltas al reloj
Pág. 73
e) La manecilla pequeña estaba en el 11 y giró 30°. ¿A qué número llegó?
Llegó al 12
f) La manecilla grande giró 30° y llegó al 8. ¿En qué número estaba?
En el número 7
g) La manecilla grande giró 90° y llegó al 3. ¿En qué número estaba?
En el número 12
h) La manecilla pequeña giró 1/2 vuelta y llegó al 9. ¿En qué número estaba?
En el número 3.
i) La manecilla grande estaba en el 6 y giró 3/4 de vuelta. ¿A qué número llegó?
Llegó al número 3.
a) La manecilla grande estaba en el 1 y llegó hasta el 4. ¿Cuántos grados giró?
90º
b) La manecilla pequeña estaba en el 9 y llegó al 12. ¿Cuántos grados giró?
90º
c) La manecilla grande estaba en el 12 y giró hasta el 6. ¿Cuántos grados giró?
180º
d) La manecilla pequeña estaba en el 2 y giró 180°. ¿Hasta qué número llegó?
Llegó al número 8
Dibuja las manecillas de cada reloj para que formen el ángulo que se indica.

41. Trazo de ángulos
Pág. 75
En parejas, sigan las indicaciones.
Tracen en una hoja blanca algunos ángulos, proponiendo las medidas. Puedes hacer el trazo de los diferentes ángulos mediante el uso de tu transportador, de la siguiente manera:Para trazar ángulosPrimero debes trazar una línea horizontal, que servirá para indicarnos 0° grados.Luego, coloca el centro del transportador en el extremo izquierdo de la línea, es decir en el punto con la letra “a”.Una vez puesto el centro del trasportador sobre el origen de la línea, y el cero grados ubicado también sobre la línea; vamos a buscar la medida del ángulo que queremos trazar, en contra de las manecillas del reloj y ponemos una marca.Y finalmente trazamos una línea del origen “a” de la línea, hacia la marca que hicimos. De esa forma obtenemos el ángulo con la medida que estábamos buscando.
continuación consigna 1
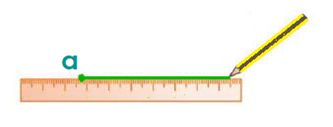
42. Cuadros o triángulos
Pág. 77
1. ¿Cuál de las siguientes figuras tiene mayor superficie?
Figura 1
2. ¿Cuál de las siguientes figuras tiene menor superficie?
Figura 4
3. ¿Qué figura tiene mayor superficie, la número 1 o la 4? expliquen su respuesta
Figura 4
4. Escriban la medida de las figuras en las siguientes tablas:
Retícula cuadradaFigura 1 19 cuadradosFigura 2 18 cuadrados
Retícula triangular Figura 3 25 triángulosFigura 4 24 triángulos
43. ¿Cuál es más útil?
Pág. 79
En equipos, elaboren las figuras.
Realizar actividad de acuerdo a los que les indique su profesorMaterialesPara cada equipo:• Papel albanene delgado,papel mantequilla, papelcebolla, papel copia opapel de china.• Las retículas (3) del material recortable, pp. 233-237.
2. 2. Ahora, sobrepongan una figura en una retícula y midan la superficie de la figura.
sobreponemos una de las figuras en una de las retículas del material recortable (pag. 233) , en este caso la figura grande en color rojo puesta sobre la retícula, midan toda la superficie.
2. Ahora, sobrepongan una figura en una retícula y midan la superficie de la figura.
sobreponemos una de las figuras en una de las retículas del material recortable (pag. 233) , en este caso la figura grande en color rojo puesta sobre la retícula, midan toda la superficie.
44. Camino a la escuela
Pág. 82
Para llegar a la escuela, Martina camina 1 350 m, Luis 875 m, Ignacio 1 418 m, Bety 918 m y Alfredo 2 130 m.
Alfredo 2 130 Dos mil ciento treintaIgnacio 1 418 Mil cuatrocientos dieciochoMartina 1 350 Mil trescientos cincuentaBety 918 Novecientos dieciochoLuis 875 Ochocientos setenta y cinco
a)¿Quién vive más cerca de la escuela, Luis o Ignacio?
Luis
b) La escuela quiere donar una bicicleta para apoyar a quien viva más lejos; si comparan los casos anteriores, ¿a quién le correspondería?
Alfredo
c) Si se juntan las distancias que caminan Martina y Bety, será____con respecto a la distancia que camina Alfredo. (Mayor a menor)
Mayor
d) ¿En qué se fijaron para ordenar los números de la tabla?
En el orden descendente
e) ¿Si sólo estuvieran escritos los nombres de los números, les serviría tomar en cuenta el número de palabras de cada número para ordenarlos?
No¿Por qué? No existe relación entre el número de palabras y el valor del número
a) ¿Para qué coche le falta menos dinero?
Auto A ¿Cuánto le falta? Cuatro mil seiscientos catorce pesos$ 4,614
b) ¿Si quisiera comprar el coche más caro, cuánto dinero le haría falta?
$ 26,594 Veintiséis mil quinientos noventa y cuatro pesos
c) ¿Qué cantidad de dinero hay de diferencia entre el coche de menos precio y el de mayor precio?
$21,980Veintiún mil novecientos ochenta pesos
45. Los cheques del jefe
Pág. 85
a) En el recuadro superior derecho anota con número la cantidad de cada cheque, según corresponda:
$ 4,020
b) ¿Quién recibió mayor sueldo?
Laura Adriana Valle
c) Expliquen cómo lo determinaron.
Cantidad de dinero que esta escrita en el cheque
d) ¿Cuál es la diferencia de dinero entre un cheque y otro? Escriban la cantidad con letra.
100 cien pesos
1. Escriban en cada cuadro el signo > (mayor que) o < (menor que), según corresponda.
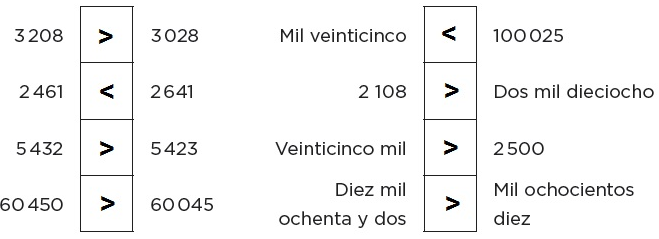
2. A partir del nombre, determinen la cantidad de cifras que tiene cada número:
a) Trescientos cuarenta y ocho 3 cifrasb) Mil nueve 4 cifrasc) Diez mil setecientos 5 cifras
46. De diferentes maneras
Pág. 88
En parejas, formulen problemas que puedan resolverse con cada expresión.
De diferentes manerasEl profesor les dara las intrucciones para que elaboren las tarjetas.Para llevar a cabo el juego en este desafío considere un tiempo de 30 minutos, aproximadamente.Se espera que los alumnos logren escribir diferentes expresiones aditivas, multiplicativas o mixtas que representen el mismo número, por ejemplo, si el número de la tarjeta es el 25, los participantes pueden escribir algunas descomposiciones como las siguientes:
47. Expresiones equivalentes
Pág. 90
1. ¿Cuántas personas pueden sentarse en la sección blanca de un auditorio si hay 4 filas con 12 butacas cada una y 3 filas con 8 butacas cada una?
72 personas
2. Al invernadero “La margarita” llegó el siguiente pedido: 3 paquetes con 30 docenas de rosas cada uno, 4 paquetes con 20 docenas de gerberas cada uno y 2 paquetes con 40 docenas de margarit
250 docenas
3. Maura está llenando bolsas de dulces para una i esta de cumpleaños. En cada bolsa mete 6 chocolates. Hasta este momento ha llenado 9 bolsas y aún quedan 18 chocolates en el paquete. ¿Cuánt
72 chocolates en el paquete
4. Éste es el registro de canastas que anotó el equipo de Luis en los últimos cuatro partidos. Si se sabe que cada canasta vale 2 puntos, ¿cuántos puntos ha acumulado el equipo?
250 puntos
5. Para pagar la entrada al cine y comprar palomitas, Fernanda y Marisol van a cooperar con $55.50 cada una, y Lorena y yo, con $69.50 cada una. ¿Cuánto dinero vamos a reunir?
$ 250 pesos
48. ¿Tienen el mismo valor?
Pág. 92
Tarjeta naranja, ¿Tienen el mismo valor?¿por qué?
No, por que el segundo valor es menor que el primero – preparatoria
Tarjeta azul, ¿Tienen el mismo valor? ¿Por qué?
No, el segundo valor es menor que el primero. – preparatoria
Tarjeta morada, ¿Tienen el mismo valor? ¿Por qué?
No, el primero resulta 5.8 y el segundo en 5.4 – preparatoria
Tarjeta roja, ¿Tienen el mismo valor? ¿Por qué?
Si, ambos valen 96 – preparatoria
Tarjeta gris, ¿Tienen el mismo valor? ¿Por qué?
Si, ambos valen 3.9 – preparatoria
Tarjeta verde, ¿Tienen el mismo valor? ¿Por qué?
No, el primero resulta 280 y el segundo en 223 – preparatoria
49. Tiras de colores
Pág. 94
1. Identifiquen a qué fracción de la tira gris corresponde cada tira de color:
TirasVerde 1/3Morada 1/6Azul 1/9Rosa 1/10Negra 1/12Amarilla 1/5Café 1/8Roja 1/2Anaranjada 1/4
Encuentren tres distintas para representar un entero don tiras de diferente color.
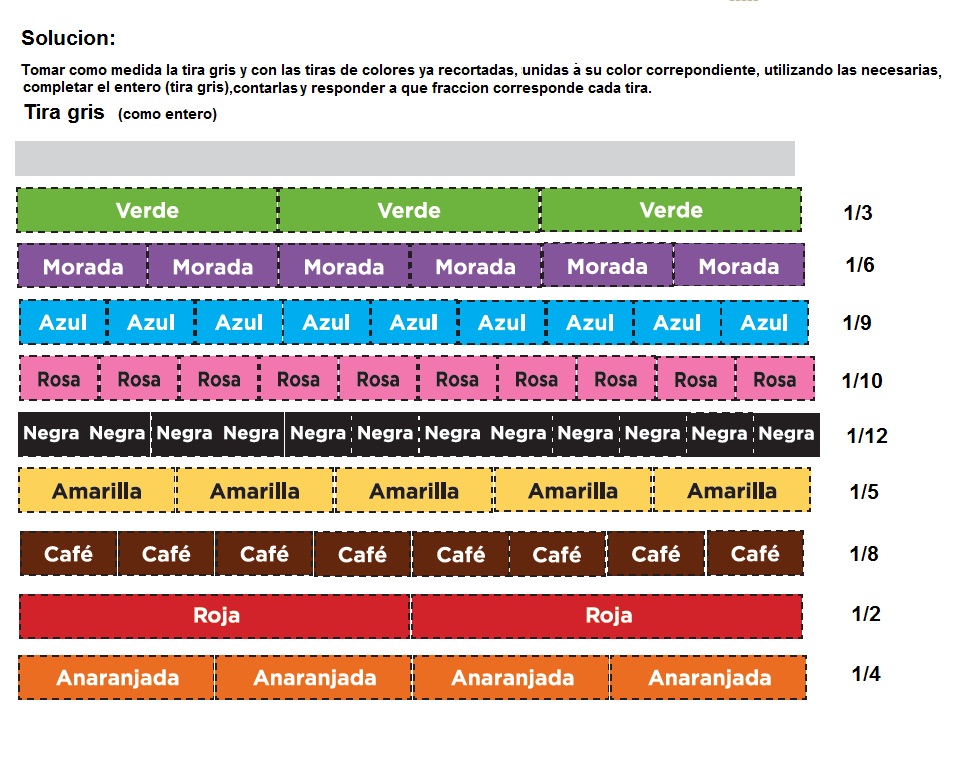
2. Encuentren tres formas distintas para representar un entero con tiras de diferente color.

3. Para cada caso, encuentren dos formas diferentes de construir 2/3 .
Representación con tiras
Con tiras del mismo colorDos verdes 1/3 + 1/3cuatro moradas 1/6 + 1/6 + 1/6 +1/6Cuatro amarillas y dos rosas 1/5 + 1/5 + 1/5 + 1/5 + 1/10 + 1/10
Con tiras de diferente colorUna verde y dos moradas 1/3 +1/3 + 1/6Una roja y una morada 1/2 + 1/6
4. Para este ejercicio deben considerar las fracciones que representan las tiras de colores; luego encuentren y anoten en el recuadro las fracciones o expresiones equivalentes posibles para c
4/5 = 1/2 + 1/5 + 1/101 2/6 = 1/2 + 1/2 + 1/6 + 1/6
Escriban sobre la línea “es equivalente a” si las dos fracciones que se comparan tienen el mismo valor. Cuando terminen, comprueben sus respuestas con las tiras de colores.
a) 6/12 es equivalente a 5/10b) 4/6 no es equivalente a 5/9c) 9/10 no es equivalente a 11/12d) 6/6 es equivalente a 10/10e) 4/3 no es equivalente a 2/2 + 1/6f) 1 3/12 no es equivalente a 3/4g) 1/2+ 1/2 no es equivalente a 7/10h) 6/8 es equivalente a 9/12
50. La fiesta sorpresa
Pág. 97
1. Jimena cumple años la próxima semana y sus amigos se organizaron para hacerle una i esta sorpresa; Jesús, Mauricio y Eduardo eligieron inflar globos de colores para jugar tiro al blanco d
La misma cantidad de cada color (3/9).por que 3/9, 6/18 y 1/3 son f, la cantidad de globos rojos y verdes es la misma y los dos juntos representan el total de globos.
2. Elisa y Talía son las encargadas de adornar el salón y para ello cada una quedó en llevar un rollo de cinta festón de 10 m.
¿Quién de las dos va a gastar más cinta? ¿Por qué? Las dos van a utilizar la misma cantidad de cintaElisa ocupó 3/5 equivalente a 6/10 (6 metros) y a talía le sobran 4 metros (4/10) quiere decir que ocupó lo mismo que elisa 6 metros.
51. Sumas y restas I
Pág. 98
1.Encuentren la fracción que sea el resultado de sumar o de restar las fracciones que se representan gráficamente.
a) 4/16 + 7/16 = 11/16b) 1 + 3/6= 1 3/6 ó 1 1/2c) 2/3 – 5/9 = 1/9
inciso d)
d) 1/10
2. En la figura en blanco, representen gráficamente la fracción que se necesita para obtener el resultado que se indica.
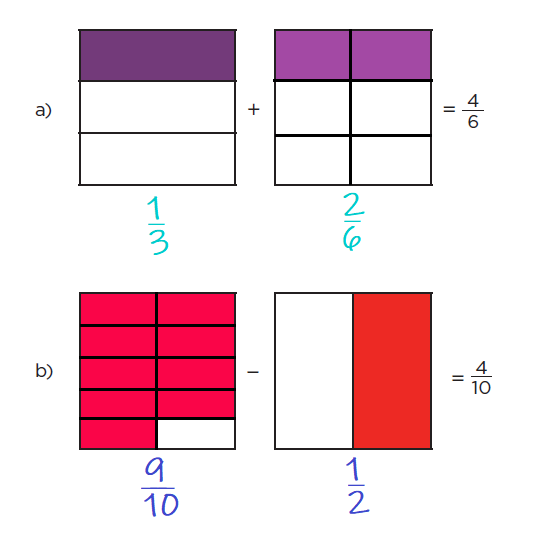
52. Sumas y restas II
Pág. 100
1.Luisa ocupa 1/3 m de listón para elaborar un moño. Si necesita 7 moños azules, 4 rojos y 5 dorados, ¿cuánto listón de cada color debe comprar
Azules: 2 1/3 equivalente a 7/3rojos: 1 1/3 equivalente a 4/3dorados: 1 2/3 equivalente a 5/3
2. En la fiesta de Saúl se sirvió helado de chocolate a todos los invitados.
3/4 litros
3. ¿Cuántos frascos y cuántas bolsas se deben colocar en el platillo derecho de la tercera balanza para mantenerla en equilibrio?
primer balanza1/2 kg + 1/2 kg
segunda balanza3/4 kg, 1/4 kg frasco + 1/2 kg bolsa = 3/4 kg
tercer balanza
2 kg , dos frascos de 3/4 kg y una bolsa de 1/2 kg
4. En 4º “A” se llevó a cabo una votación para elegir al representante del grupo.
1/6 del grupo
53. Los ramos de rosas
Pág. 102
1. El sábado, don Gustavo vendió en el mercado 15 ramos con 12 rosas cada uno. ¿Cuántas rosas vendió?
180 rosas
2. El domingo hizo ramos con 24 rosas cada uno y vendió 14 ramos. ¿Cuántas rosas vendió?
336 rosas
3. Don Gustavo vende los ramos de 12 rosas a $15 y los de 24 rosas a $25.
a) 225 pesosb) 350 pesos
4. En su parcela tiene 28 surcos con 23 rosales en cada uno. ¿Cuántos rosales tiene en total?
644 rosales
54. Cuadrículas grandes y pequeñas
Pág. 103
Anoten los números que faltan y la multiplicación que le corresponde a cada una.
4 x5 = 208 X 5= 404 X 7 = 288 X 7= 565 X 12 = ( 5 X 4) + ( 5 X 8 ) = 608 X 12 = ( 8 X 7) + ( 8 X 5) = 96
Continuación…
4 x 12 = (4 x 7) + (4 x 5) = 487 x 12 = ( 7 x 8) + ( 7 x 4 ) = 8412 x 12 = (4 x 5) + ( 4 x 7 ) + ( 8 x 5 ) + ( 8 x 7) = 144
55. Multiplicación con rectángulos
Pág. 105
Obtengan el resultado de las siguientes multiplicaciones
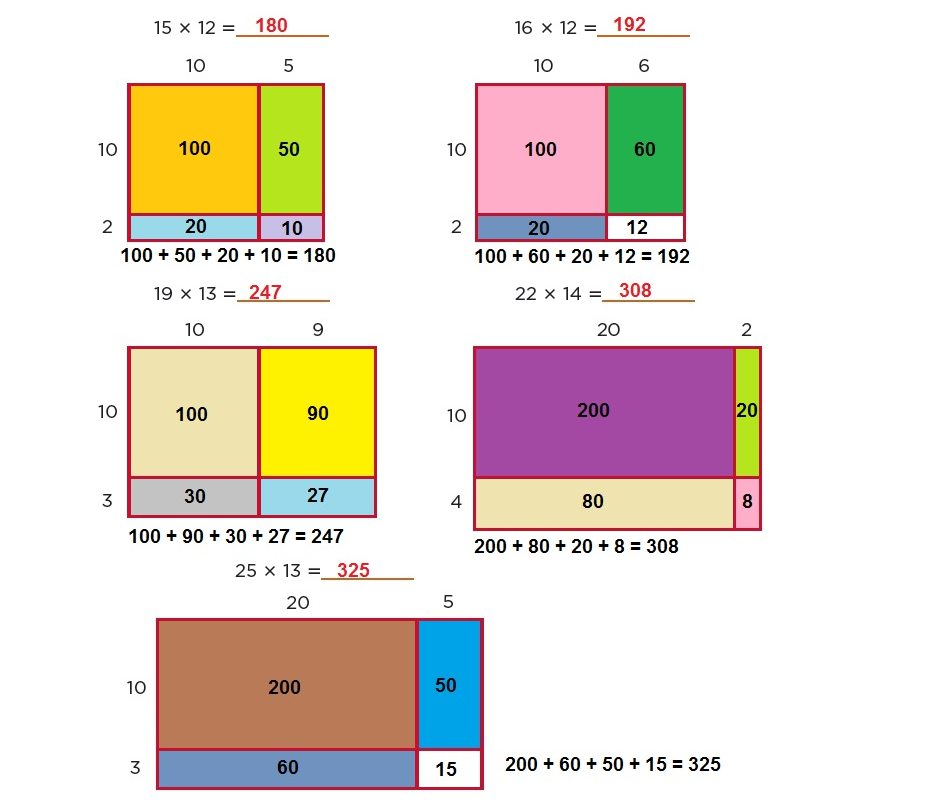
56. La multiplicación
Pág. 106
Anoten los números que faltan en algunas partes de los rectángulos y en las cuentas.
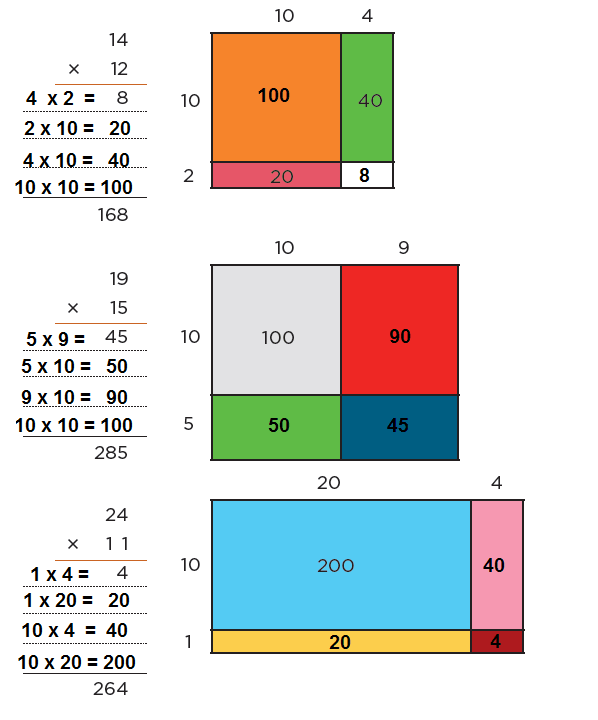
57. Algo simple
Pág. 107
Anoten los números que faltan en las operaciones…
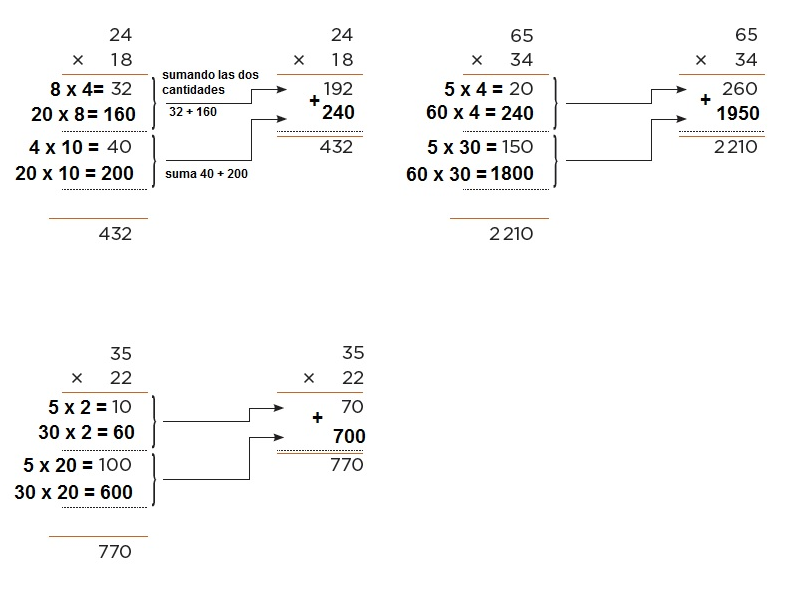
58. Hagamos cuentas
Pág. 108
a) Para ir a México a Cuautla, Jullian gastó $ 150 en gasolina, $ 218 en caseta de cobro y $65 en una comida. ¿Cuánto gastó en total?
$ 433 pesos
b) El día que Julián fue a Cuautla llevaba $500, ¿Cuánto le sobró?
$67 pesos
c) Julián debe ir de México a Cuautla durante 15 sábados: va y regresa en su coche el mismo día y sólo come una vez en Cuautla. ¿Cuánto dunero va a gastar Julián en transporte ..
$ 5, 475 pesos
d) El automóvil de Julián recorre aproximadamente 12 km por cada litro de gasolina. ¿Cuántos litros necesitaría para recorrer 180 km?
15 litros
d) El automóvil de Julián recorre aproximadamente 12 km por cada litro de gasolina.
15 litros
59. De viaje
Pág. 109
De acuerdo con las distancias marcadas, ¿Cúal de los tres dias don javier recorrió más kilómetros?
1er día 530 km2do día 459 km3er día 470 km
60. En la feria
Pág. 110
1. La rueda de la fortuna da 12 vueltas cada vez que se echa a andar. En la mañana del sábado se echó a andar 5 veces, y por la tarde 16 veces más. ¿ Cuántas vueltas dio en total?
b) 5 x 12 + 16 x 12c) 21 x 12
2. Al cabo de una semana, la rueda de la fortuna dio 25 vueltas por dia, en promedio. Si continúa con este ritmo. ¿Cuáantas vueltas habrá dado en un mes?
dos solucionesa) 25 x 7 x 4 + 2 x 25b) 25 x 7 + 25 x 7 + 25 x 7 + 25 x 7 + 2 x 25d) 30 x 25
3.La rueda de la fortuna tiene 14 canastillas, y en cada una pueden subir 2 personas. Si todas las canastillas se ocupan, ¿Cuántas personas habrán subido después de 8 vueltas?
b) 14 x 8 x 2d) 28 x 8
y despues de 25 vueltas, ¿Cuántas habrán subido? a) 25 x 2 x 14b) 28 x 25
4. El viernes se vendieron 80 boletos para la rueda de la fortuna: 37 para niños y 43 para adultos…
a) 37 x 15 + 43 x 20c) 30 x 15 + 7 x 15 + 40 x 20 + 3 x 20
61. Cuadriláteros
Pág. 112
En equipo, desarrollen la actividad.
Te recomiendo que visites la siguiente página para comprender qué son los cuadriláteros:
62. ¿En qué se parecen?
Pág. 113
Observen el pliego de papel del profesor que muestra los cuadriláteros de la sesión anterior.
Te recomiendo que visites la siguiente página para recordar cuáles son los cuadriláteros:
63. Los habitantes de México
Pág. 114
En equipos contesten las preguntas que se plantean en los dos problemas siguientes.
Te recomiendo visites la siguiente página para poder comprender mejor esta lección
a) ¿Qué estado de la república mexicana tiene el mayor número de habitantes?
Estado de México
b) ¿ Cuál es la entidad con menor número de habitantes?
Baja California Sur
c) Si se suma, por una parte, la población de las entidades que se encuentran en la frontera del norte y , por otra, las de la frontera sur, ¿Cuáles reunen más habitantes?
Frontera Norte
d) ¿Cuál es la diferencia en número de habitantes entre la entidad más poblada y la menos poblada?
14,538,836
e) Busquen la entidad en la que viven y anoten el número de habitantes que se reportó en el censo de 2010.
3,406,465
f) ¿Cuáles son las entidades que tienen menos de un millón de habitantes?
Baja California Sur, Campeche, Colima
a) ¿Cuál era la esperanza de vida en 1930?
33.9 años
b) ¿Cuántos años en promedio podía vivir la generación del año 2000?
75.3 años
c) ¿Cuántos años ha aumentado la esperanza de vida de 1950 a 2010?
28.5 años
d) ¿Creen que el tipo de alimentación influya para que la esperanza de vida haya aumentado tanto en las últimas décadas?¿Por qué?
Sisi mejora la alimentación, mejora la salud de las personas y por lo tanto, la esperanza de vida
e) ¿Qué aspectos consideran que puedan influir para que la esperanza de vida aumente?
Comer saludablemente
64. Cuida tu alimentación
Pág. 117
En equipos contesten las preguntas.
Antes de empezar, te recomiendo que visites la siguiente página, para refrescar los conocimientos de la sesión pasada:
a)¿En qué grupo hay más alumnos con problemas de sobrepeso?
En primer grado
b) ¿Consideran que hay más riesgo de sobrepeso en las niñas que en los niños?¿Por qué?
Si,¿Por qué? la respuesta dependera de cada alumno
c) ¿Qué se vende más en la cooperativa de la escuela?
Dulces
d) ¿Creen que haya alguna relación entre el problema de sobrepeso y lo que consumen los niños de esta escuela¿Por qué?
Si, por que entre más comida chatarra, más probabilidad hay de tener sobrepeso.
e) Además de la alimentación, en su estancia en la escuela, ¿qué sugerencias les darían a sus compañeros para disminuir el problema del sobrepeso?
Hacer ejercicio regularmente
65. ¿Qué parte es?
Pág. 120
1.Completen la siguiente tabla para determinar la cantidad de la producción que se vendió a cada distribuidor.
propias, impropias y mixtas
2. Una familia compró un taxi; el papá aportó $ 80 000, la mamá $ 40 000, y el hijo será quien lo maneje.
propias, impropias y mixtas
66. ¿Qué fracción es?
Pág. 122
1. En un grupo de 4° grado compraron rosas y claveles para obsequiarlas el 10 de mayo. De acuerdo con la ilustración, ¿qué fracción del total de fl ores son claveles?
5/20 ó 1/4
equivalentes
2. Juan está completando su álbum de animales acuáticos, de felinos y de aves; la siguiente ilustración representa las estampas que tiene repetidas. ¿Qué fracción del total de estampas repeti
equivalentes
3. En la siguiente tabla se registraron los vehículos que pasaron por una caseta de cobro en dos horas distintas de un día. Escriban la fracción que le corresponde a cada tipo de auto, de acu
equivalentes
67. ¿Cuántos eran?
Pág. 124
1. El equipo que está en una actividad con la maestro David representa la séptima parte del grupo; ¿cuántos alumnos hay en ese grupo?
21 alumnos
2. Este año, en el zoológico se observó que la población de patos correspondía a las 2/5 partes del total de la población de aves acuáticas. Si hay 36 patos, ¿cuál es el total de aves acuátic
90 aves acuáticas propias, impropias y mixtas
3. En una bodega había cajas con frascos de frutas y verduras en conserva. Del total de frascos, 2/3 tenían fresas, la cuarta parte duraznos, y también había 2 frascos de chiles y zanahorias,
a) ¿Cuántos frascos había en las cajas? 24 frascos
b) ¿Cuántos frascos había de cada producto? 16 de fresas, 6 de duraznos,, 2 de chiles y zanahorias
propias, impropias y mixtas
68. ¡Primero fíjate si va!
Pág. 125
En equipos, determinen en cada caso si la figura de la derecha corresponde o no a la sucesión de figuras. En caso ai rmativo, escriban qué lugar le corresponde.
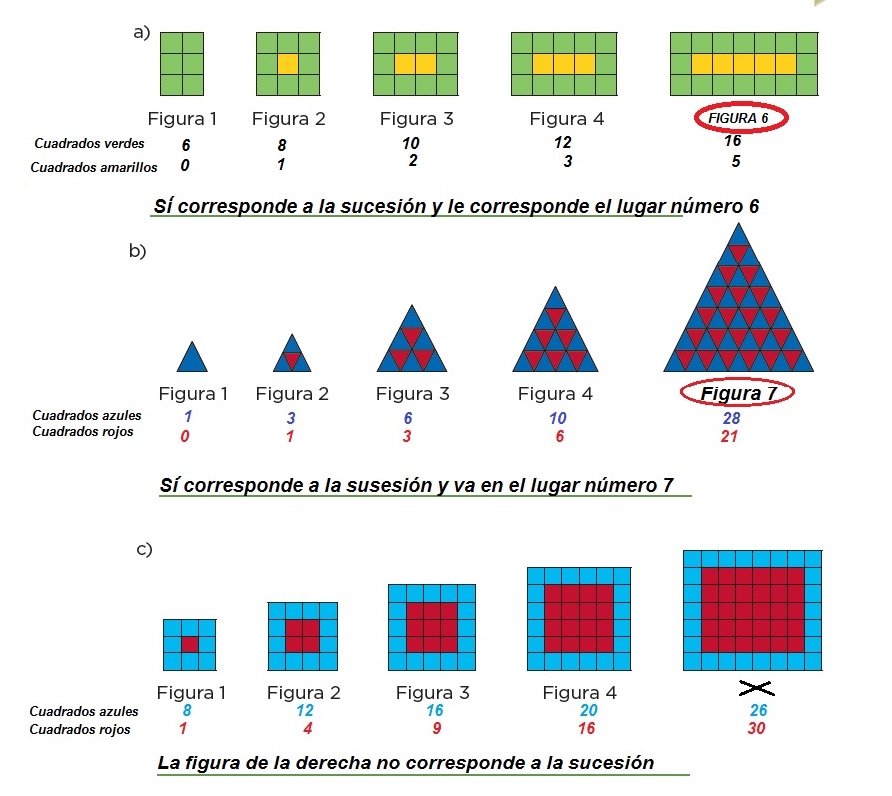
69. Estructuras de vidrio
Pág. 126
A Diego le encargaron armar estructuras de vidrio para la fachada de un edii cio. Las piezas que necesita son: hojas de vidrio cuadrado, tubo metálico y sujetadores.
a) ¿Cuántos tubos metálicos y cuántos sujetadores necesita Diegopara hacer una estructura con 5 hojas de vidrio? 16 tubos metálicos y 12 sujetadores
b) ¿Cuántos tubos metálicos y cuántos sujetadores necesita Diegopara hacer una estructura con 10 hojas de vidrio? 31 tubos metálicos y 22 sujetadores
¿Cuántos cuadrados de color café y de color beige se necesitan para armar una estructura de 30 piezas en total y que corresponda con la sucesión? ¿Cuál es el perímetro de esta estructura de 30?
Se requieren 22 piezas color beige y 8 piezas de color café con perímetro de 26 cm
70. De varias formas
Pág. 128
1. La siguiente sucesión numérica corresponde al número de cuadrados verdes y azules de la sucesión de fi guras. ¿Cuáles son los cuatro términos que continúan esta sucesión?
6 ,0, 8, 1, 10, 2, 12, 3, 14, 4, 16, 5
2. Escriban la sucesión numérica que corresponde al número de cuadrados azules y rojos de la siguiente sucesión de figuras:
8, 1, 12, 4, 16, 9, 20, 16a) ¿Los números 5 y 10 corresponden a la sucesión numérica? nob) ¿Cuántos cuadrados azules tendrá la figura 5 de la sucesión? 24 azules¿Y cuadrados rojos? 25 rojos
a) ¿Los números 5 y 10 corresponden a la sucesión numérica?
No
1. Escriban dos sucesiones de números que sean compuestas y que tengan 8 términos.
8, 1, 12, 4, 16, 9, 20, 16,…
71. Problemas olímpicos
Pág. 130
a) ¿Cuál es la diferencia entre el largo del caballo y el largo de la barra de equilibrio?
3.4 m
b) ¿Cuántos centímetros mide el ancho de cada barra asimétrica?
7 cm
c) ¿Cuántos centímetros es más ancho el caballo que la barra de equilibrio?
25 cm
d) ¿Cuál es la diferencia entre la altura de las dos barras asimétricas?
.85 m
a) ¿Cuál es la distancia entre la línea de tiro libre y la línea de media cancha?
8.2 m
b) ¿Qué distancia hay entre las dos líneas de tiro libre?
16.4 m
c) Si un jugador logra encestar desde la línea de media cancha, ¿cuál es la longitud de su tiro?
12.8 m
d) ¿Cuál es la medida del ancho de la cancha?
15m
Organizados en parejas escriban los signos >, < o =, para comparar estas expresiones.
a) 8.15 m < 12.87 m – 4.68 mb) 4.60 m > 0.25 m + 3.48 m + 0.50 mc) 63 cm + 78 cm + 59 cm < 2.08 md) 8 dm + 35 dm > 3.30 me) 3.52 m = 35 dm + 2 cm
72. Cambiemos decimales
Pág. 133
En equipos hagan los ejercicios

73. Son equivalentes
Pág. 134
1.Registren en las líneas las expresiones fraccionarias y decimales que representan el mismo valor
I. a,lII. b,g y tIII. e, n y rIV. f, jV. c, sVI. d, kVII. h,mVIII. o,pIX. i,q
2. Escriban el número que esta formado por
a) 15 décimos, 12 centésimos y 17 milésimos15/10 = 1.5, 12/100 = .12, 17/1000= .0171.5+0.12+.0017= 1.637
b) 432 milésimos, 23 centésimos y 39 décimos.432 + 0.23 + 3.9 = 4.562
c) 25 décimos y 128 milésimos2.5 + 0.128 = 2.628
d) 43 décimos y 7 milésimos4.3 + 0.007 = 4.307
e) 6 décimos y 3 centésimos0.6 + 0.03 = .63
74. La medida de sus lados
Pág. 136
tabla
Morado 21 7 3Rosa 126 18 7Gris 84 12 7Azul 48 16 3Amarillo 162 18 9Verde 44 11 4Rojo 85 17 5
75. ¿Habrá otro?
Pág. 138
Hay 354 losetas para cubrir el piso de un salón de la escuela. Después de hacer algunos cálculos, los trabajadores se dieron cuenta de que les conviene acomodarlas en filas de 9 losetas. ¿Cu
El procedimiento que hizo el equipo de Felipe es el más largo, ya que fué descontado de uno en uno y los hizo más complicado.
a) ¿Qué diferencias observan entre los cálculos que hicieron los equipos de Rosa y de Felipe?
El procedimiento que hizo el equipo de Felipe es más largo ya que fue descontado de uno en uno y los hizo más complicado.
b) ¿Cuál de los tres cálculos consideran que es el más rápido?
El equipo de Luis,¿por qué? El equipo de Luis hizo un cálculo parecido al de Rosa, la diferencia fué que el equipo de Luis desconto en cada intento grupos con multiplos de 10 ó de 1 , mayores a los de Rosa , por eso logro ser el procedimiento más corto y por lo tanto más rápido.
c) ¿Podrían hacer un cálculo aún más corto que el del equipo de Luis?
Si, si inician quitando las losetas de las 30 filas en un solo intento, y posteriormente quiten las losetas de 9 filas en lugar de 5 y 4 filas por separado.
76. Lo que hace falta
Pág. 141
En parejas, escriban en los espacios los datos necesarios para cada división resulte correcta.

operaciones
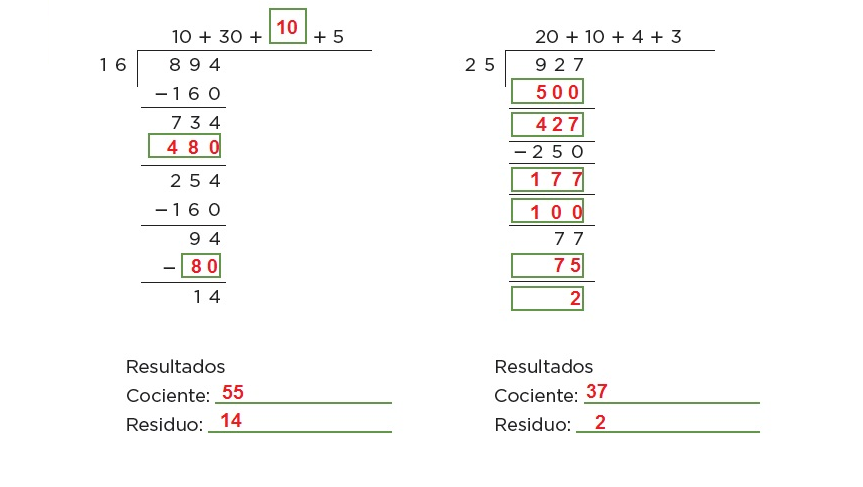
77. ¡Mucho ojo!
Pág. 143
En parejas , revisen estas divisiones. Si encuentran que en alguna hay errores, desarrollenla correctamente en su cuaderno.

78. De práctica
Pág. 144
En parejas, analicen estas divisiones. Después describan en las líneas cómo las resolvieron.
CONSIGNA 1 : Expresar con sus propias palabras lo que observan y como lo relacionan con los procedimientos analizados. Divisiones
Individualmente, resuelve estas divisiones siguiendo el procedimiento que describiste en la consigna 1.
Divisiones
79. ¿Cuántas veces cabe?
Pág. 146
1. Consideren el cuadrado pequeño como unidad de medida y calculen la medida del contorno..

2. Rafael y Carmela están discutiendo acerca del perímetro y del área de las siguientes dos i guras, pero no se ponen de acuerdo. Rafael dice que la i gura 1 tiene mayor perímetro y mayor área
Carmela esta en lo correcto ya que la figura 1 tiene 16 unidades de perímetro y 7 de área. Por otro lado, la figura 2 tiene 14 unidades de perímetro y 8 de área.
En pareja, resuelvan los problemas.

80. Contorno y superficie
Pág. 149
1. Dibujen en la cuadrícula
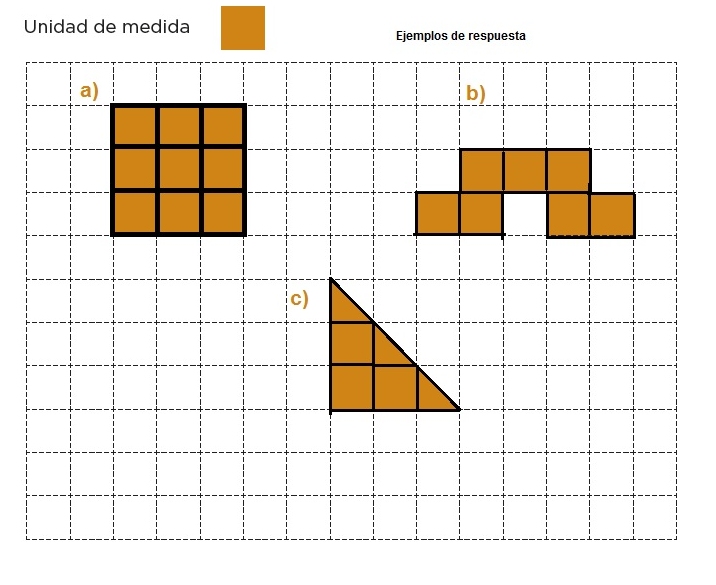
2. Para el trazo del inciso c, cuatro alumnos dibujaron las siguientes figuras; verifiquen si cumplen o no con la condición y escriban por qué.
Alumno 1 4.5 UnidadesAlumno 2 4.5 UnidadesAlumno 3 4 UnidadesAlumno 4 4.5 Unidades
El alumno 1, 2 y 4 estan correctos , sólo el alumno 3 no cumplió con la condición ya que contando los cuadrados y las mitades en total , sólo quedan en 4 unidades.
81. Relación perímetro-área
Pág. 151
1. Utilicen la siguiente cuadrícula para dibujar 2 figuras distintas que tengan el mismo perímetro pero diferentes áreas.
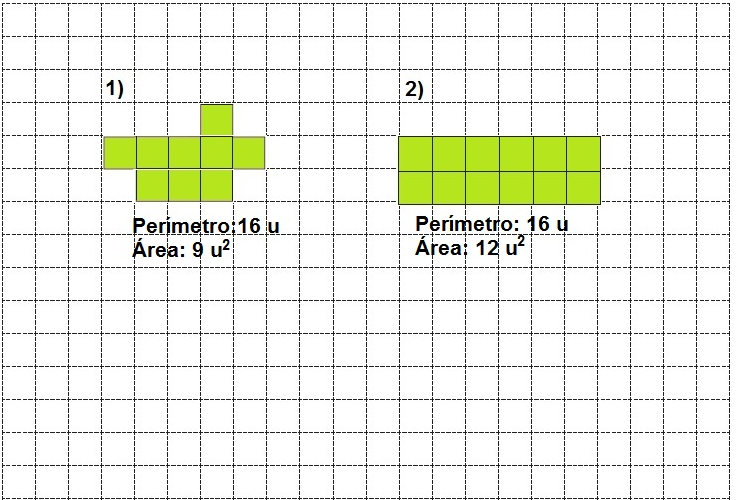
2. Utilicen la siguiente cuadrícula para dibujar 2 i guras distintas que tengan la misma área pero diferentes perímetros.
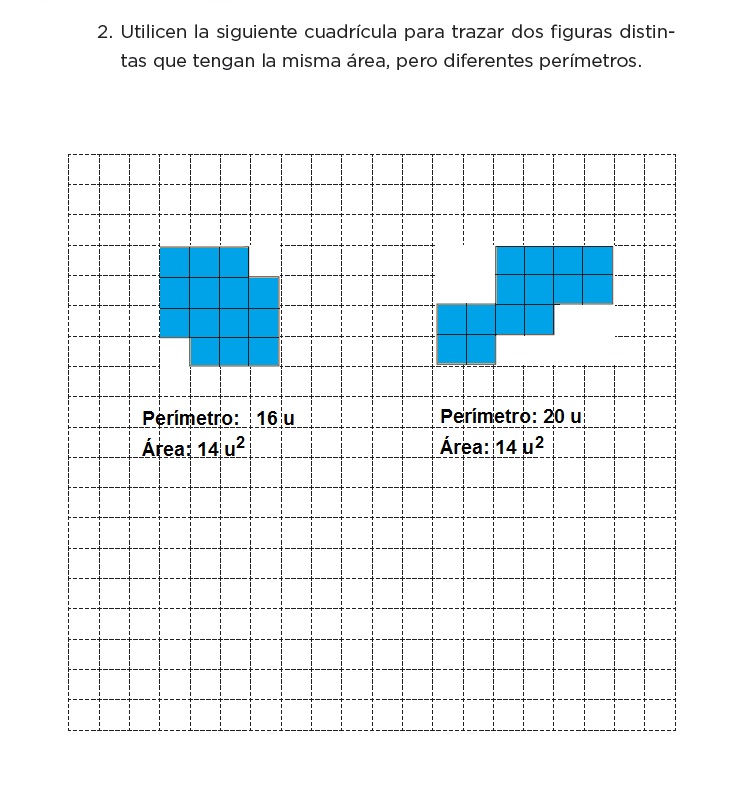
3. ¿Habrá 2 figuras diferentes que tengan el mismo perímetro y la misma área? Intenten dibujarlas en la siguiente cuadrícula.
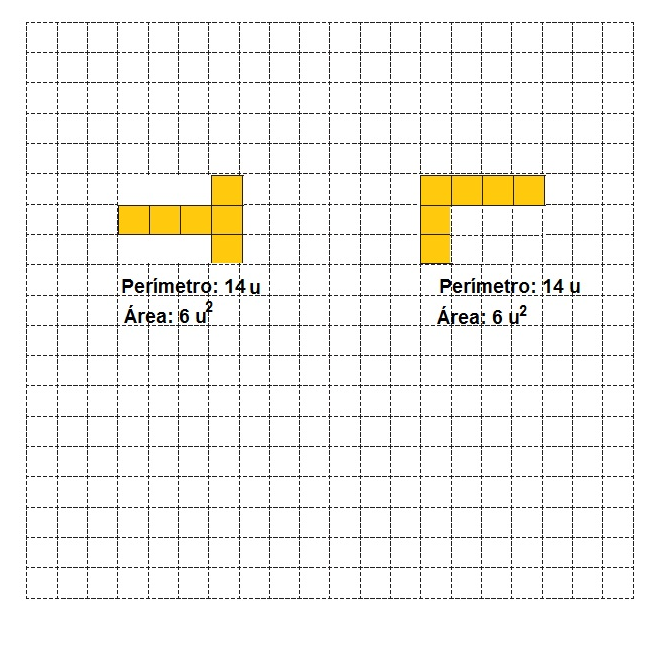
83. Las costuras de Paula
Pág. 155
1. Paula hace servilletas y manteles de tela, y para decorarlos les cose encaje en toda la orilla. ¿Cuánto encaje necesita para un mantel que mide 2.5 m de largo y 1.5 m de ancho?
8 metros
¿Qué hicieron para calcular la cantidad de encaje que necesitaPaula?
sumando todos sus lados (sacando su perímetro)
2. En el grupo de Rogelio también resolvieron el problema. Su equipo contestó que para encontrar el resultado, ellos sumaron el doble del largo más el doble del ancho del mantel.
¿Creen que ese procedimiento sea correcto? Si¿Por qué? Por que de esta manera se suman todos los lados de la figura con lo que se obtiene el perímetro.
3. Resuelvan este problema siguiendo el procedimiento del equipo de Rogelio
¿Cuánto encaje necesita Paula para decorar una servilleta quemide 80 cm de largo y 45 cm de ancho? 2.5 metros
4. ¿Cómo expresarían de forma breve ese procedimiento?
Comentalo con tus propias palabras
84. ¿Cuántos caben?
Pág. 157
1. Don Julio tiene una huerta de manzanos distribuidos en 11 filas, cada una con 9 árboles, ¿cuántos árboles tiene en total? Expliquen cómo obtuvieron este resultado:
99 árboles
2. El papá de Ana va a colocar adoquín cuadrado en el patio de su casa. ¿Cuántos adoquines necesitará para cubrir todo el patio, si caben 15 hileras de 30 adoquines cada una? Expliquen cómo o
450 adoquines
3. La pared de un baño está cubierta con 360 azulejos que miden dm2; si la pared tiene 24 filas, ¿cuántos azulejos tiene cada fila?
15 azulejos
85. Superficies rectangulares
Pág. 158
En equipos, con su material listo, formen cuatro rectángulos diferentes que tengan un área de 40 cm2. Registren en la tabla las medidas de sus rectángulos.

La tabla de abajo contiene información de diferentes rectángulos; escriban los datos que faltan para completarla.
¿Cómo supieron qué números faltaban? Respuesta del alumno.
86. En busca de una fórmula
Pág. 160
En parejas, realicen estas actividades. Anoten la medida de la superficie de cada rectángulo.
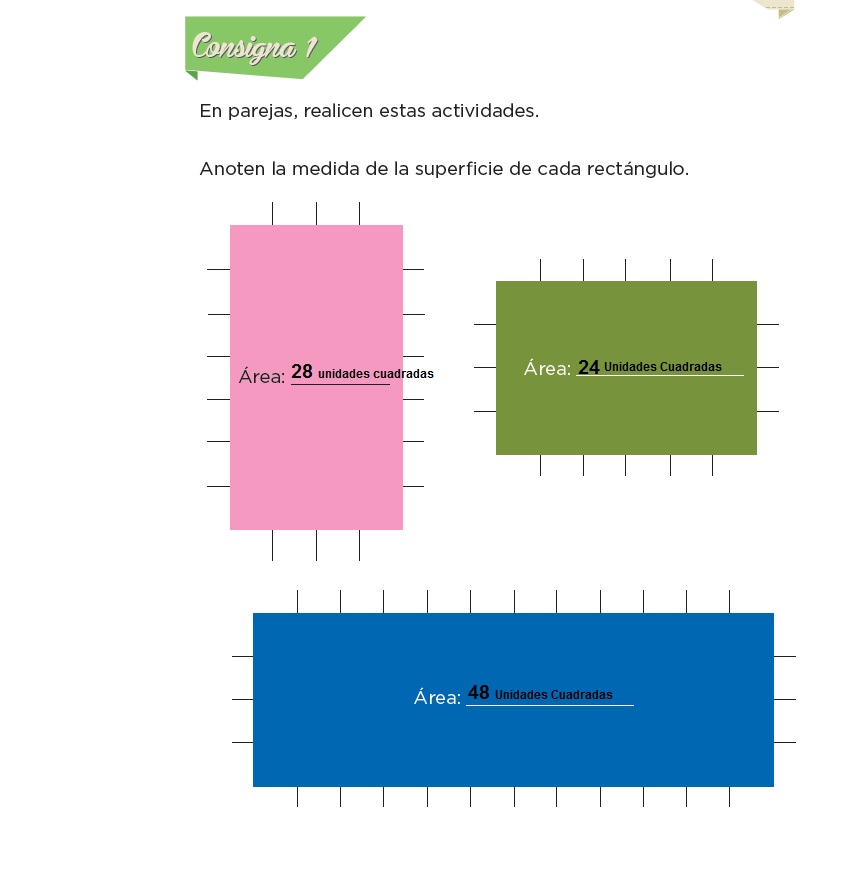
Continuación de las medidas
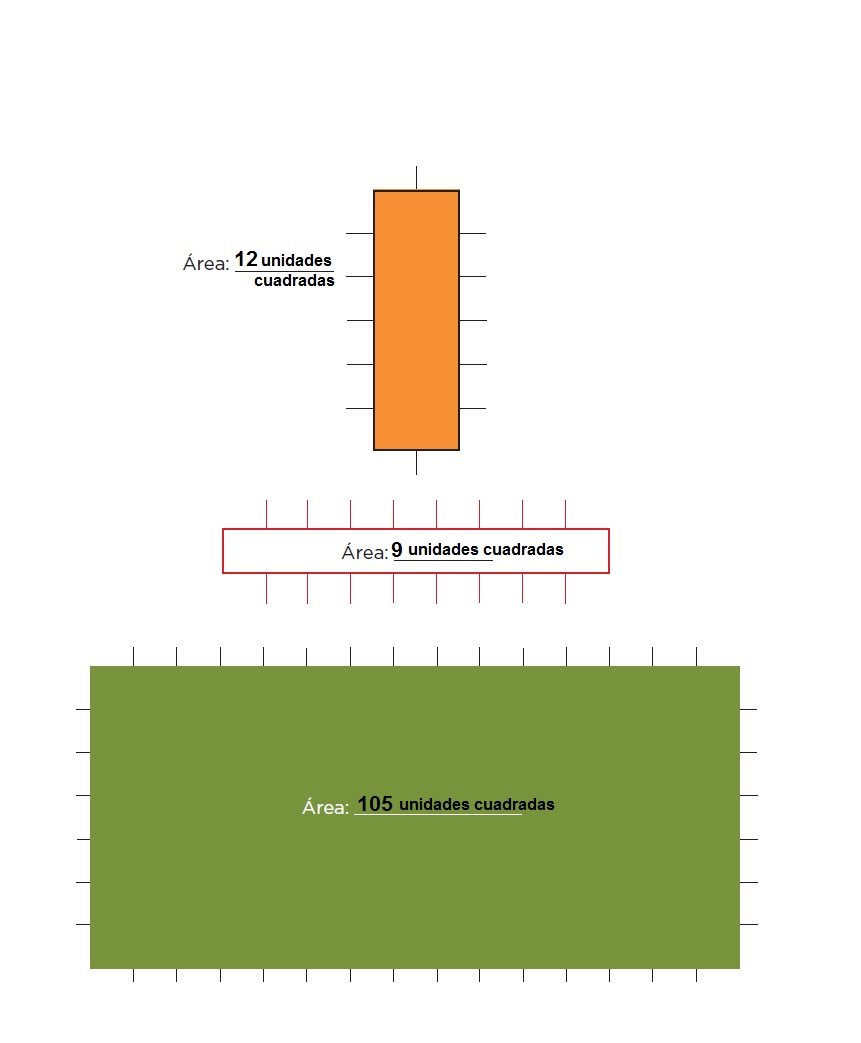
Tracen y coloreen en la cuadrícula 4 rectángulos con las medidas que se indican.

Continuación
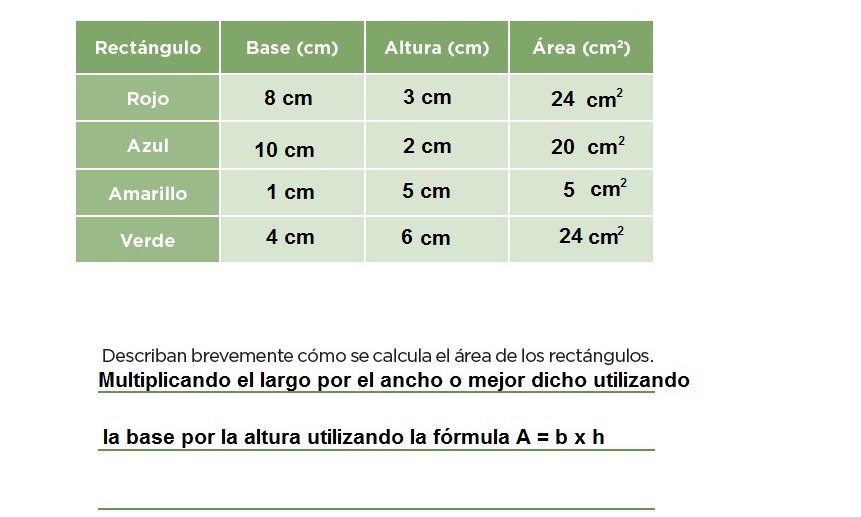
87. Medidas en el salón de clases
Pág. 164
1. Estimen el área de las superficies que se indican, y después utilicen los cuadrados que construyeron (con indicaciones de su maestro) para medirlas
Es una actividad para realizar en físico, pero te recomiendo que revises las siguientes ligas para completar el tema.
2. Utilicen al menos dos unidades de medida diferentes para medir las superficies.
Es una actividad para realizar en físico, pero te recomiendo que revises las siguientes ligas para completar el tema.
88. ¿Cómo es?
Pág. 166
Utilicen los cuadrados del desafío anterior y construyan una figura que corresponda a cada una de estas medidas:
Es una actividad para realizar en físico, pero te recomiendo que revises las siguientes ligas para completar el tema.
89. ¿Por qué son iguales?
Pág. 168
Instrucciones
La consigna consiste en que cada alumno se encargue de representar una fracción; si se considera conveniente, de acuerdo con las características de los alumnos, se integran parejas para representar algunas fracciones.En consignas anteriores los alumnos representaron e identiicaron fracciones equivalentes mediante diversos recursos. Ahora se trata de que ellos establezcan una forma para identiicarlas y generarlas; en este caso, se espera que adviertan que multiplicando el numerador y el denominador de una fracción por un mismo número natural, se obtiene una fracción equivalente a ella. equivalentesDivisión de
90. Sólo del mismo valor
Pág. 170
1. Escriban los números que faltan para que las fracciones de cada grupo sean equivalentes:
equivalentesDivisión de
2. Encierren en un círculo las fracciones que son equivalentes con la primera de la izquierda.
a) 8/36 , 4/18b) 3/9, 1/3c) 2/3, 4/6 equivalentes, decimales y equivalencias
91. El número mayor
Pág. 171
1. Compara las fracciones y coloca el signo > o <, según sea el caso.
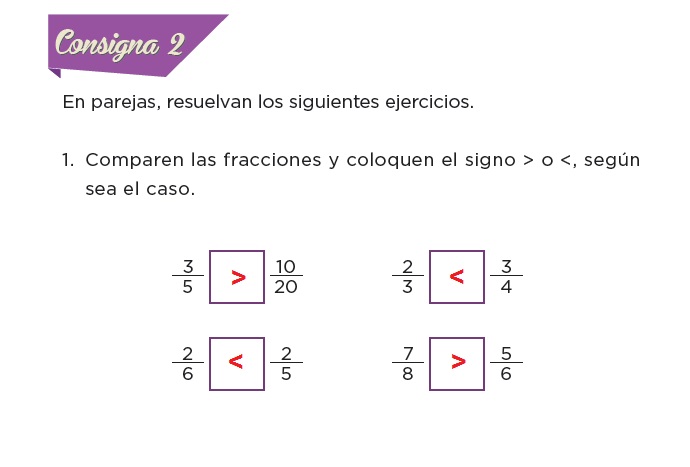
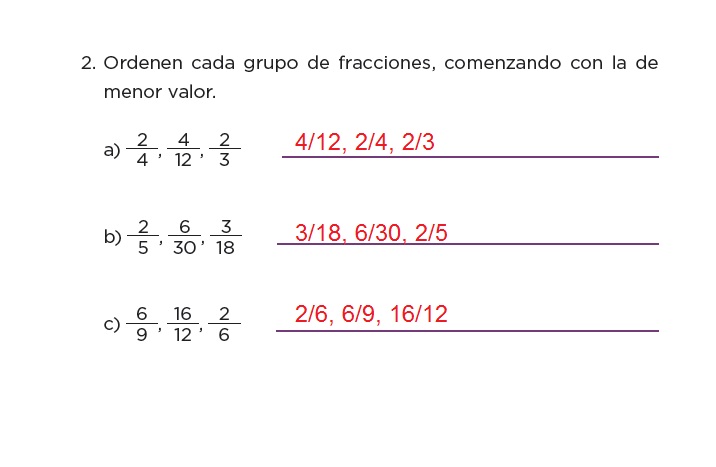
2. Ordena cada grupo de fracciones, e inicia con la de menor valor.
94. Dobles, triples, cuádruples
Pág. 175
a) ¿Cómo se obtiene el número de cuadros de una figura a partir de la anterior?
Se obtiene multiplicando el número de cuadros de la figura anterior x 4.
b)¿Cúal es la regularidad del número de cuadros de cada figura de la sucesión?
4 veces el número anterior.
c) ¿Cuál es la sucesión numérica que se genera con el número de cuadros de cada figura?
1,4,16,64
d) Si se continúa la sucesión, ¿cuántos cuadros tendría la figura 5?
256 cuadros
a) ¿Cómo se obtiene el número de triángulos de una figura a partir de la sucesión anterior?
Se obtiene multiplicando el número de cuadros de la figura anterior por 4
b) ¿Cuál es la regularidad del número de triángulos de cada figura de la sucesión?
4 veces el número anterior.
c) ¿Cuál es la sucesión numérica que se genera con el número de triángulos de cada figura?
1,4,16,64
d) Si se continúa la sucesión, ¿cuántos triángulos tendría la figura 5?
256
95. Sucesión con factor
Pág. 177
a) ¿Cuál es la sucesión numérica que representa el número de cuadros verdes?
8,12,20,36Cúal es la regularidad de esta sucesión: El número que se va sumando es el doble que el anterior, esto se observa en los números en rojo 8+4 =12 , 12+8=20, 20+16=36
b) ¿Cúal es la sucesión numérica que representan los cuadros amarillos?
1,4,16,64
¿Cuál es la regularidad de esta sucesión? El número de cuadros amarillos para cualquier figura se obtiene multiplicando el número de cuadros amarillos de la figura anterior por 4.
2.Los números que están abajo de cada cuadrado representan la medida de cada uno de sus lados.
a) Si se continúa la sucesión de cuadrados, ¿cuánto miden porlado los cuadrados de las figuras 6, 7 y 8, respectivamente?
64, 128, 256
b) La siguiente sucesión representa el área del triángulo de coloren cada cuadrado. ¿Cuáles son los números que faltan?
2, 8, 32, 128, 512, 2048 , 8 192,
c) ¿Cuántos cuadros amarillos tendrá la figura 6?
1024¿Y la figura 7? 4096¿Y cuántos cuadros verdes tendrán cada una de esas figuras? 132 fig. 6 y 260 fig. 7
96. No basta con mirar
Pág. 179
a) ¿Cuál es la sucesión numérica que representa el número de cuadrados que tienen por lado las i guras?
2,4,8,16
b) ¿Cuál es la sucesión numérica que representa el área de los cuadrados?
4 ,16 ,64 ,256
c) ¿Cuál será el área del cuadrado que ocuparía el lugar 5 en la sucesión?
1024
d) ¿La siguiente figura corresponde a la sucesión? ¿Por qué?
No.
por que el 10 (número de cuadrados por lado) y el 100 (área del cuadrado) no corresponden a la sucesión de cuadrados.
a) ¿Cuál es la regularidad que observan de la sucesión de fi guras?
El área de la figura es 4 veces el área de la figura anterior, el área morada es la mitad del área total de la figura, se alterna el área de la figura.
b) ¿Cuál es la sucesión numérica que representa el área de los triángulos sombreados?
2,8, 32, 128
c) ¿Cuál será el área que tendrá el triángulo sombreado en la figura 5 de la sucesión?
512
¿Por qué? Por que la sucesión es de multiplos de 4, se multiplica el número anterior por 4.
d) ¿La siguiente figura corresponde a la sucesión?¿Por qué?
No.
Por que tiene un número non por lado y esta sucesión incluye unicamente números pares múltiplos de 4.
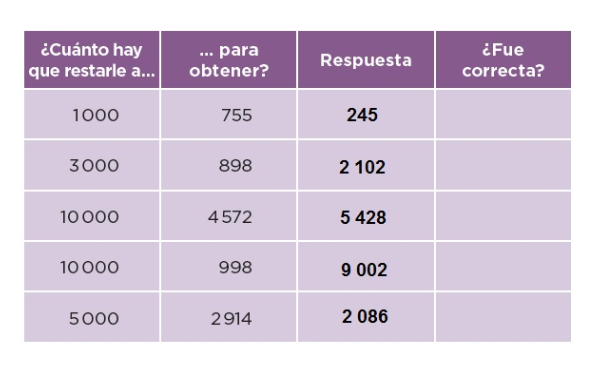
97. ¿Cuánto le falta?
Pág. 183
En parejas, desarrollen la actividad.

Ahora, analicen y completen lo que se solicita en la tabla 2.
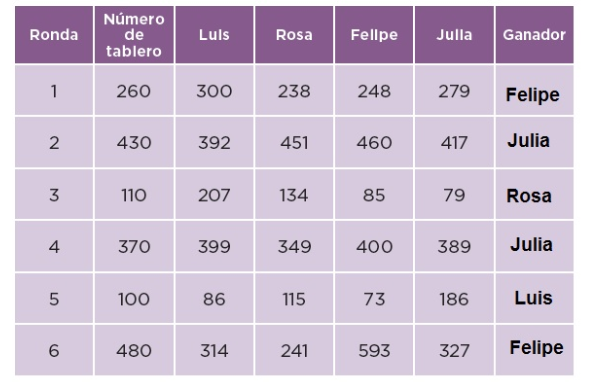
98. Los más cercanos
Pág. 185
Resuelve este problema; para decidir cada respuesta haz los cálculos mentalmente.
99. De frutas y verduras
Pág. 186
a) Si están preparando dos ensaladas, ¿qué ingredientes agregarían para que cada una contenga las calorías indicadas? Escriban sobre las líneas.
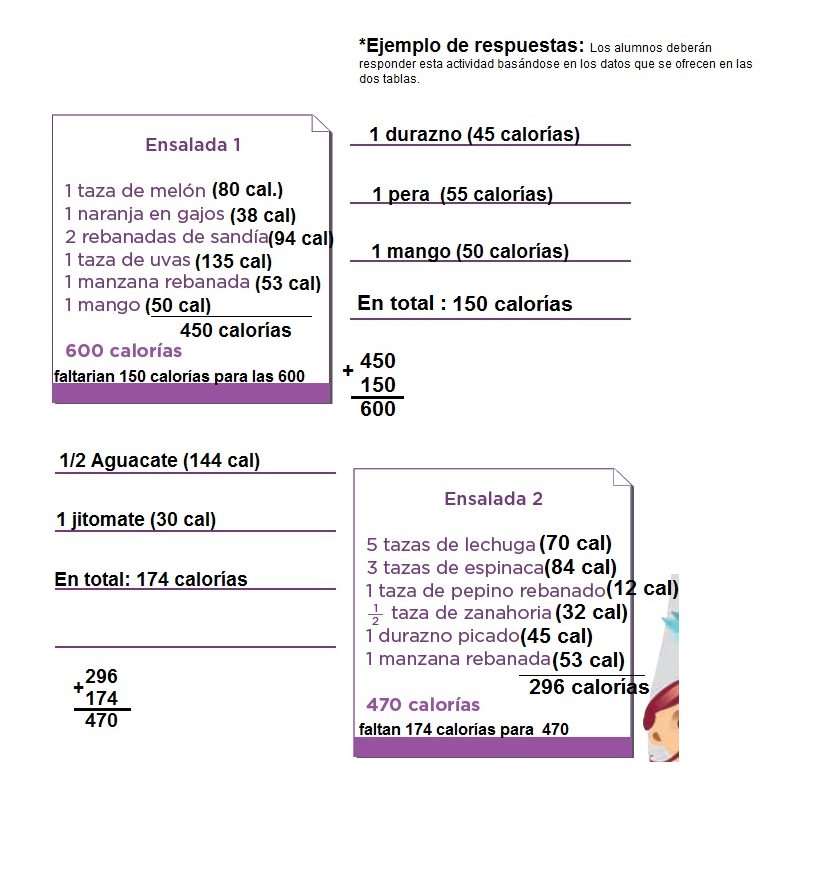
Con tu mismo compañero, calculen cuál es la diferencia de calorías entre los grupos de alimentos que están separados por una diagonal
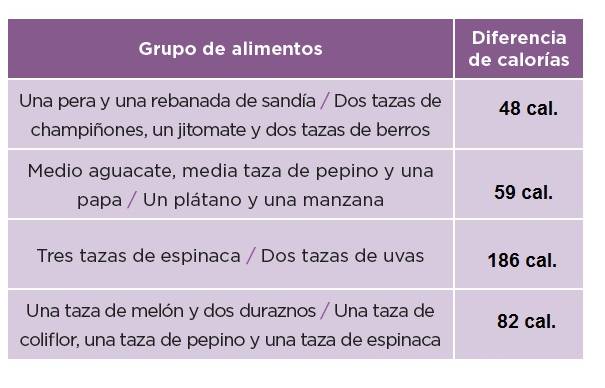
100. ¡Nos vamos de excursión!
Pág. 189
a) si deciden la primera opción, ¿cuántos autos se van a necesitar para el paseo?
9 autos
b) En esa cantidad de autos, ¿podrían ir solamente 4 niños en cada uno?
No, se necesitan 2 auto más
¿Por qué?
Por que 7 alumnos quedarian fuera de los 9 autos, agregando un auto más se puede transportar 4 niños más y sobrarían 3 niños, entonces se necesitaría un auto más aunque en éste no viajaría la misma cantidad de niños que en el resto de los autos.
c) Si deciden la segunda opción, ¿cuántas camionetas se necesitarían?
6 camiones
d) Cuatro alumnos quieren invitar a un hermano; si el profesor acepta, ¿sería necesario disponer de más camionetas?
No es necesario más camionetas.
¿Por qué? Por que en la sexta camioneta hay 5 lugares disponibles
e) ¿Cuántos niños más se podrían invitar para ocupar todos los lugares disponibles en los autos?
2 niños más
¿Y para ocupar todos los lugares disponibles en las camionetas?
5 niños más
101. Libros y cajas
Pág. 191
El empleado de una librería tiene que empacar 368 libros del mismo tamaño. Si en una caja caben 24 libros:
a) ¿Cuántas cajas se requieren para empaquetar todos los libros?
16 cajas
b) ¿Cuántos libros más se podrían empaquetar, de tal manera que todas las cajas estén totalmente llenas?
16 libros más
c) Se podrían empaquetar los libros de manera que en todas las cajas haya la misma cantidad? ¿Por qué? Si, si en cada una de las 16 cajas se empaquetan 23 libros, ningun libro queda fuera, por lo que sí hay otra manera de guardarlos .
d) Si entre los libros hay seis de Matemáticas, ¿podría ocuparse una de las cajas solamente con estos libros? ¿Por qué? No , en 15 cajas caben 360 libros y para cumplir con esta condición se necesitaría espacio para 362 libros.
102. ¿A cuál le cabe más?
Pág. 192
En equipos, lleven a cabo la actividad; el maestro les entregará un recipiente grande y uno pequeño.
a)¿Cuántas veces creen que quepa el agua del recipiente menor en el mayor? Esta actividad se realizara usando un recipiente que el maestro les entregara.
105. ¡Pasteles, pasteles!
Pág. 195
En la pastelería “Delicias”, don Roque registró la venta de rebanadas de pastel de los primeros días de la semana:
a) ¿Qué día se vendieron más rebanadas de pastel de zanahoria? El miércoles
b) ¿Cuántas rebanadas de pastel de queso se vendieron el díalunes? 9 rebanadas
¿Y el día martes? 9 rebanadas
¿Y el miércoles? 14 rebanadas
c) ¿De qué pastel se vendieron menos rebanadas durante lostres días, de fresa o de tres leches? Tres leches
d) ¿De qué pastel se vendieron más rebanadas el día lunes? Chocolate
¿Y el martes? Chocolate
¿Y el miércoles? Queso
e) Don Roque tiene que hacer más pasteles para la venta del díajueves, ¿de qué sabores le conviene hornear más? ¿Por qué?
Chocolate y queso , por que son los que se venden más.
106. Cuando la moda se acomoda
Pág. 197
1. Éstas son las calificaciones del tercer bimestre de Jesús y de Mariano
a) ¿Cuál es la moda de las calificaciones de Mariano y cuál es la moda de las calificaciones de Jesús? 7 de Mariano y 7 de Jesús
b) Según las calificaciones de todas sus materias, ¿quién tuvo mejor rendimiento en el tercer bimestre? Mariano
c) ¿Creen que la moda de las calificaciones de Jesús y de Mariano es útil para determinar quién tuvo mejor rendimiento? ¿Por qué?
No, por que no se toma en cuenta el resto de las calificaciones
2.En la tienda “La paloma” se venden uniformes escolares. La señora Irma, encargada de la tienda, elaboró un registro de los suéteres de secundaria vendidos en una semana.
a) ¿Cuál es la moda de las tallas de suéter? talla 12 b) ¿Servirá de algo conocer la moda en el registro de la señora Irma? Si¿Para qué? Conocerla ayuda al vendedor de uniformes a solicitar más piezas de una determinada talla y al fabricante a producirlas en mayor cantidad que las otras.



