La hipótesis nula (H 0 ) es la ba sis de prueba de hipótesis estadísticas. Es la hipótesis predeterminada (que se supone verdadera) la que establece que no existe una diferencia estadísticamente significativa entre algún parámetro de la población (como la media) y un valor hipotetizado. Por lo general, se basa en análisis o conocimientos previos.
La hipótesis nula se utiliza para varios propósitos, como verificar supuestos estadísticos, verificar que múltiples experimentos están produciendo resultados consistentes, avanzar directamente teorías y más.
Más comúnmente, la hipótesis nula se usa para establecer la igualdad entre dos o más variables, como un medicamento y un placebo. Luego, esta igualdad se prueba en una prueba de hipótesis estadística. Generalmente, la hipótesis nula es la hipótesis que el investigador intenta refutar, aunque no siempre es necesariamente el objetivo. Se contrasta con la hipótesis alternativa (H a ), que es una afirmación de que existe alguna diferencia (el valor es mayor, menor o no igual), y busca proporcionar evidencia de que cualquier Las diferencias observadas son estadísticamente significativas y no se deben a variaciones aleatorias.
Por ejemplo, la hipótesis nula puede afirmar que el GPA de los estudiantes de una escuela secundaria determinada es no mejor que el promedio estatal. La hipótesis alternativa correspondiente puede establecer que el GPA de los estudiantes de una escuela secundaria determinada es mejor que el promedio estatal, y luego se realizaría una prueba de hipótesis para determinar si hay evidencia suficiente para rechazar la hipótesis nula a favor de la hipótesis alternativa.
Notación
Matemáticamente, la hipótesis nula se denota como H 0 y se expresa como
H 0 : μ=μ 0
donde μ 0 es la media poblacional asumida o hipotetizada, y μ es la media de la población de la que se extraen las muestras. Dado que la hipótesis nula es una afirmación de que no hay diferencia entre estos parámetros de población,
μ – μ 0 =0
La hipótesis alternativa generalmente adopta una de estas tres formas:
| H a : μ & gt; μ 0 |
| H a : μ & lt; μ 0 |
| H a : μ ≠ μ 0 |
H 0 también se puede indicar como una desigualdad:
H 0 : μ & gt; μ 0
La hipótesis alternativa correspondiente se establece como:
H a : μ ≤ μ 0
Prueba de hipótesis estadística
Una prueba de hipótesis estadística se adhiere al siguiente procedimiento general:
- Indique las hipótesis nula y alternativa.
- Seleccione un nivel de significancia, α (la probabilidad de rechazar la hipótesis nula cuando la hipótesis nula es verdadera) y la estadística de prueba apropiada.
- Realice la prueba adecuada y determine la región crítica de la distribución correspondiente.
- prueba z
- prueba t
- prueba de chi-cuadrado
- Prueba F
- Calcule el valor observado de la estadística de prueba.
- Rechace la hipótesis nula a favor de la hipótesis alternativa si el valor observado se encuentra dentro de la región crítica. De lo contrario, no rechace la hipótesis nula.
Alternativamente, en lugar de usar regiones críticas, es posible calcular el valor p y compararlo con el nivel de significancia elegido:
- Si el valor p es menor o igual al nivel de significancia, rechazar la hipótesis nula a favor de la hipótesis alternativa.
- Si el valor p es mayor que el nivel de significancia, no lo rechace la hipótesis nula.
Tenga en cuenta que el objetivo de este tipo de prueba de hipótesis es determinar si existe evidencia para rechazar la hipótesis nula a favor de la hipótesis alternativa en un nivel de significancia dado. Esto no es lo mismo que probar o aceptar una hipótesis alternativa, ya que puede haber evidencia para la hipótesis alternativa en un nivel de significancia, pero no en otro. Además, si no hay evidencia suficiente para la hipótesis alternativa, no rechazamos la hipótesis nula, en lugar de aceptarla; no es posible aceptar la hipótesis nula.
Ejemplo
El puntaje promedio nacional del SAT, calculado para todos los estudiantes del tercer año, fue de 1150 con una desviación estándar de 75. Una muestra de 35 estudiantes del tercer año de una escuela secundaria determinada tuvo un puntaje promedio de 1250. Suponiendo un nivel de significancia de 0.05, use una prueba Z para determinar si la diferencia entre el puntaje promedio de la clase de 35 y el promedio nacional es estadísticamente significativa.
1. Enuncie las hipótesis nula y alternativa:
H 0 : μ=1150
H a : μ ≠ 1150
2. El nivel de significancia seleccionado es 0.05 y las puntuaciones de las pruebas siguen una distribución normal, por lo que es apropiado calcular la puntuación Z de la estadística de prueba y realizar una prueba Z.
3. Dado que queremos determinar si existe alguna diferencia, una prueba de dos colas es apropiada, lo que significa que la región crítica de 0.05 se divide en dos regiones críticas que comprenden un área de 0.025 cada una; las regiones críticas para una prueba Z de dos colas dado un nivel de significancia de 0.05 son:
Z & lt; -1,96 y Z & gt; 1,96
4. Calcule la puntuación Z del valor observado:
5. Dado que la puntuación Z del valor observado no se encuentra dentro de la región crítica (como se muestra en la figura siguiente), no rechazamos la hipótesis nula.
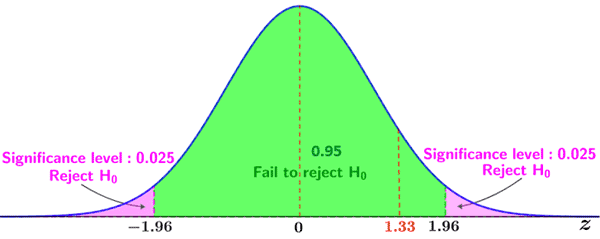
No rechazar la hipótesis nula sugiere que no existe una diferencia estadísticamente significativa entre los puntajes promedio de la clase de 35 y el promedio nacional a un nivel de significancia de 0.05.
Un nivel de significancia α de 0.05 significa que existe un 5% de probabilidad de rechazar la hipótesis nula cuando la hipótesis nula es verdadera. Cuando esto ocurre, el error se denomina error de tipo I o falso positivo. En los casos en que ocurre lo contrario y no rechazamos la hipótesis nula cuando es falsa, se denomina error de tipo II, como se resume en la siguiente tabla:
| H 0 es cierto | H 0 es falso | |
|---|---|---|
| Rechazar H 0 | Error de tipo I | Inferencia correcta |
| No se pudo rechazar H 0 | Inferencia correcta | Error de tipo II |



