La geometría es una rama de las matemáticas que incluye el estudio de forma , tamaño y otras propiedades de las figuras. Es una de las ramas más antiguas de las matemáticas y puede que se haya utilizado incluso en tiempos prehistóricos. Podemos producir figuras geométricas a partir de situaciones de la vida real. A continuación se muestra una imagen con puntos , líneas y planos . representan las paredes y los componentes estructurales de los edificios.

La geometría a menudo se divide en geometría plana y geometría sólida.
Geometría plana
La geometría plana incluye el estudio de puntos, líneas y figuras geométricas como círculos y polígonos que se encuentran en un avión.
Hay tres términos en geometría que se usan ampliamente y que realmente no se pueden definir usando objetos bien definidos. Sin embargo, existe un acuerdo general sobre lo que significan; es decir, las definiciones de estos términos son axiomáticas. Son la base para crear y trabajar con cualquier figura geométrica.
Señalar
Un punto indica una ubicación en el espacio. No tiene dimensión y está representado por un punto. Los puntos suelen estar etiquetados con letras mayúsculas.
• Un
punto A
Línea
Una línea tiene una dimensión, su longitud, y se representa con una línea que contiene flechas que indican que se extiende en cualquier dirección de forma indefinida. Dos puntos que no se superponen determinan una línea única y podemos nombrar la línea con esos dos puntos o con otros dos puntos en la línea.
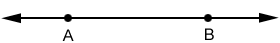
línea o
Avión
Un avión tiene dos dimensiones, largo y ancho, y forma una superficie plana (como un trozo de papel de cuaderno) que se extiende en ambas direcciones de forma indefinida. Un plano puede ser nombrado por tres puntos no colineales o por una letra.

Plano ABC o plano P
Las formas formadas en geometría plana tienen perímetro y área si son polígonos, circunferencia y el área si son círculos y la longitud si son unidimensionales, como una línea.
Geometría sólida
La geometría sólida es la rama de la geometría que estudia figuras sólidas (tridimensionales ). Los sólidos son poliedros (plural de poliedro) o no poliedros.
Poliedro
Un poliedro es un sólido cuyas caras son polígonos.
 |  | |
| Octaedro cuyas caras son triángulos | Prisma rectangular cuyas caras son rectángulos. |
No poliedro
Un no poliedro es un sólido que tiene superficies total o parcialmente curvadas.
 |  | |
| Un cono recto tiene una base circular que se estrecha hacia una punta. | La superficie de una esfera es completamente redonda como una pelota. |
Las formas formadas en geometría sólida tienen volumen y área de superficie . También puede medir la longitud de una parte de un sólido, como la longitud de un borde de un prisma rectangular o el radio de una esfera.
Tipos de geometría
Existen numerosas ramas de la geometría que se clasifican en función de varios criterios, como los métodos de estudio, los tipos de objetos estudiados y más. Las siguientes son algunas de dichas ramas:
Geometría analítica
La geometría analítica es el estudio de la geometría plana y sólida que utiliza álgebra e incorpora el plano de coordenadas o plano de coordenadas tridimensional. A veces se la denomina geometría de coordenadas por este motivo.
Dado que la geometría analítica usa álgebra y los planos de coordenadas para figuras geométricas, tiende a ser de naturaleza más numérica y, por lo tanto, ha demostrado ser una rama importante de las matemáticas utilizada por ingenieros y físicos.
Geometría euclidiana
La geometría euclidiana es el estudio de la geometría plana y sólida que utiliza axiomas, postulados y razonamiento deductivo para demostrar teoremas sobre conceptos geométricos.
¿Sabías que?
El tipo de geometría que la mayoría de los estudiantes suelen estudiar se registró en The Elements , un conjunto de libros escritos por Euclides alrededor del año 300 a. C. un matemático griego. Ahora también existen otros tipos de geometría. Estos otros tipos se originaron unos 2000 años después del trabajo de Euclides.
Geometría no euclidiana
La geometría no euclidiana generalmente usa la mayoría de las ideas de la geometría euclidiana, pero usa una versión diferente del postulado paralelo de Euclides. En la geometría euclidiana, dos líneas paralelas nunca se cruzan. En la geometría no euclidiana, las líneas paralelas pueden cruzarse según el tipo de geometría que se elija. Hay dos tipos básicos: geometrías esféricas e hiperbólicas no euclidianas.
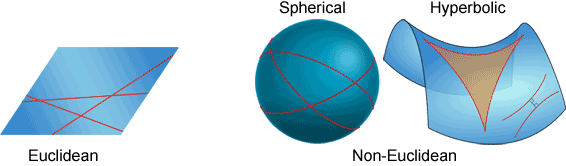
Piense en doblar un plano en geometría euclidiana sobre una esfera o un hiperboloide (una hipérbola tridimensional). Las líneas son curvas y circulares o elípticas en geometría esférica, y parabólicas o hiperbólicas en geometría hiperbólica.



