El área de un hexágono es el espacio contenido dentro de su perímetro . El espacio gris es el área del hexágono en la siguiente figura.
Fórmula del área de un hexágono regular
Hay muchos tipos diferentes de hexágonos. El tipo más común es un hexágono regular, que es un hexágono que tiene lados de igual longitud y ángulos de igual medida.
El área, A, de un hexágono regular se puede encontrar dada solo la longitud de su lado, s, con la fórmula:
Ejemplo:
Calcula el área de un hexágono regular que tiene un perímetro de 72.
Dado que el perímetro es 72, la longitud de cada lado del hexágono regular se puede encontrar dividiendo el perímetro entre 6, lo que hace que cada lado tenga una longitud de 12.
Colocando la longitud del lado en la fórmula del área:
A veces, en la vida real, es más fácil medir la distancia entre lados opuestos de un hexágono regular. En tal caso, el área del hexágono es:

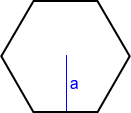
La apotema, a, de un hexágono regular es la mitad de la distancia entre los lados opuestos del hexágono. La fórmula del área que utiliza la apotema es:
Encontrar área usando una cuadrícula
Otra forma de encontrar el área de un hexágono es determinar cuántos cuadrados unitarios se necesitan para cubrir su superficie. A continuación se muestra un cuadrado unitario con longitudes laterales de 1 cm.
Se puede usar una cuadrícula de unidades cuadrados para determinar el área de un hexágono.
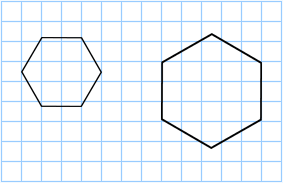
La cuadrícula de arriba contiene cuadrados unitarios que tienen un área de 1 cm 2 cada uno. El hexágono regular de la izquierda contiene 6 cuadrados completos y 10 cuadrados parciales, por lo que tiene un área de aproximadamente:
El hexágono regular a la derecha contiene 17 cuadrados completos y 10 cuadrados parciales, por lo que tiene un área de aproximadamente:
Este método se puede utilizar para encontrar el área de cualquier forma; no se limita a hexágonos regulares. Sin embargo, es solo un valor aproximado del área. Cuanto más pequeña sea la unidad cuadrada utilizada, mayor será la precisión de la aproximación. Usar una cuadrícula formada por cuadrados de 1 mm es 10 veces más preciso que usar una cuadrícula formada por cuadrados de 1 cm.
Derivación de la fórmula del área

Divide el hexágono regular en seis triángulos equiláteros dibujando segmentos de línea en vértices opuestos. Cada triángulo tiene una longitud de lado sy una altura (también la apotema del hexágono regular) de . El área, A, de uno de los triángulos equiláteros, dibujados en azul, se puede encontrar usando:



