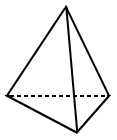
En Geometría, un poliedro es una figura espacial cerrada cuyas caras son polígonos . La palabra poliedro tiene orígenes griegos, es decir, muchas caras. Los siguientes son algunos ejemplos de poliedros.
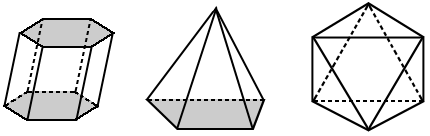
Características de un poliedro
Los polígonos que forman un poliedro se llaman caras. Los segmentos de línea creados por dos caras que se cruzan se denominan aristas. Los vértices son puntos donde se encuentran tres o más aristas.
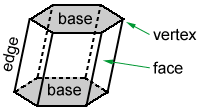
El prisma hexagonal de arriba es un poliedro que tiene 6 caras laterales que son paralelogramos y 2 caras en la parte superior e inferior, llamadas bases, que son hexágonos.
Teorema de Euler
El teorema de Euler muestra una relación entre el número de caras, vértices y aristas de un poliedro. Establece que la suma de las caras y los vértices menos el número de aristas siempre es igual a dos:
F + V – E=2
donde F es el número de caras, V es el número de vértices y E es el número de aristas de un poliedro.
Ejemplo:
Para el prisma hexagonal que se muestra arriba, F=8 (seis caras laterales + dos bases), V=12 y E=18:
8 + 12 – 18=2
Clasificaciones de poliedros
Los poliedros se pueden clasificar de muchas formas. Por ejemplo, se pueden clasificar en poliedros regulares e irregulares. Un poliedro regular es un poliedro cuyas caras son todas polígonos regulares congruentes; cualquier poliedro que no cumpla estas condiciones se considera irregular.
Los poliedros también se pueden clasificar como convexos y cóncavos. Un poliedro cóncavo tiene al menos una cara que es un polígono cóncavo. Un poliedro que no es cóncavo, es convexo. Los poliedros también se pueden clasificar según el número de caras que tiene. Por ejemplo, un tetraedro tiene 4 caras, un pentaedro tiene 5 caras y un hexaedro tiene 6 caras.
La siguiente es una lista de términos que se usan con frecuencia para describir los poliedros en función de sus características.
Prismas
Los prismas son poliedros que tienen dos caras congruentes, llamadas bases, que se encuentran en planos paralelos. Un prisma se denomina típicamente por la forma de sus bases poligonales. Las caras laterales (los lados que no son bases) son paralelogramos , rectángulos o cuadrados .
| Prisma regular | Prisma irregular |
|---|---|
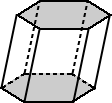 | 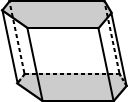 |
| Las bases del prisma hexagonal regular anterior tienen bases que son hexágonos regulares. | Las bases del prisma hexagonal de arriba son un hexágono irregular. |
Pirámides
Las pirámides son poliedros que tienen un polígono como base y triángulos como todas las demás caras. Una pirámide también se suele nombrar por la forma de su base poligonal.
| Pirámide regular | Pirámide irregular |
|---|---|
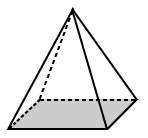 | 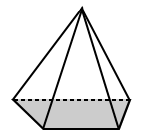 |
| La base de la pirámide cuadrada de arriba tiene una base que es un cuadrado (un polígono regular). | La base de la pirámide trapezoidal de arriba es un trapezoide con lados desiguales (por lo que es un polígono irregular). |
Poliedros regulares
Un poliedro regular es un poliedro cuyas caras son polígonos regulares congruentes. Un poliedro regular se nombra en función de su número de caras. Solo hay cinco poliedros que son poliedros regulares; estos se conocen como sólidos platónicos.
Los cinco sólidos platónicos
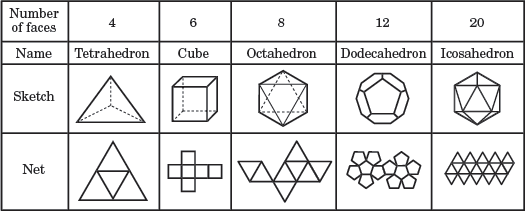
En el diagrama anterior, cada poliedro regular se nombra en función de su número de caras. La red debajo de cada boceto muestra una imagen 2D de todas las caras del poliedro.
La mayoría de los prismas regulares generalmente no se consideran poliedros regulares. Un cubo es el único prisma regular que también se puede clasificar como poliedro regular.
Del mismo modo, un tetraedro regular es la única pirámide regular que también es un poliedro regular.