El análisis de regresión es un proceso utilizado para estudiar conjuntos de datos con el fin de determinar si existe alguna relación. Se puede considerar como la mejor suposición de la tendencia que siguen los datos y puede ser útil para hacer predicciones sobre los datos.
La regresión lineal es la forma más común de análisis de regresión. Sin embargo, hay muchas formas diferentes de regresión, como regresión logarítmica, regresión sinusoidal, regresión polinomial y más. En su nivel más básico, el análisis de regresión se divide en regresión lineal o no lineal:
| Regresión lineal | Regresión no lineal |
|---|---|
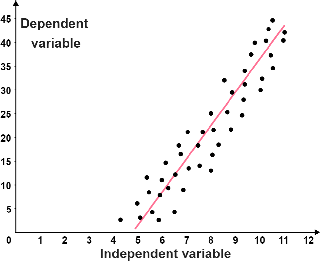 | 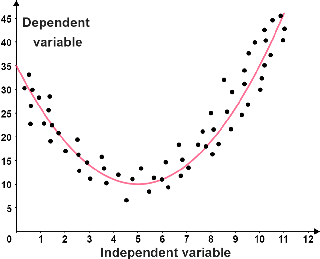 |
| Los datos siguen una tendencia lineal. La línea roja se conoce como la línea de mejor ajuste; representa mejor la relación entre los puntos. | Los datos siguen una tendencia no lineal. La línea de mejor ajuste es una parábola, por lo que los datos son cuadráticos. |
Regresión lineal simple y múltiple
Un modelo de regresión lineal intenta mostrar una relación lineal entre una variable independiente y una variable dependiente ; predice el valor de la variable dependiente en función de la variable independiente. Hay dos tipos de regresión lineal: regresión lineal simple y regresión lineal múltiple.
Regresión lineal simple
Un modelo de regresión lineal simple tiene solo una variable independiente y una variable dependiente, en lugar de tener múltiples variables independientes. Por ejemplo, se podría usar una regresión lineal simple para predecir la distancia que puede viajar un automóvil en función del tamaño de su tanque de gasolina. En este caso, la variable dependiente es la distancia y la variable independiente es el tamaño del tanque de gasolina.
Las regresiones lineales simples se pueden modelar usando la siguiente ecuación
donde x es la variable independiente, es la variable dependiente, β 0 es el valor inicial de la variable dependiente, y β 1 es el cambio en la variable dependiente por cada cambio de unidad en la variable independiente.
Gráficamente, el modelo es una línea con intersección y en β 0 y una pendiente de β 1 . La variable dependiente, , también conocida como el valor esperado, es el resultado esperado del experimento para un determinado valor de x.
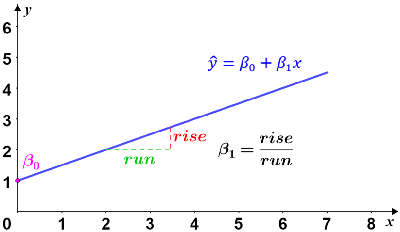
Las regresiones lineales simples comúnmente usan el método de mínimos cuadrados ordinarios para estimar la línea de mejor ajuste. No importa cuán preciso sea, siempre habrá algún grado de variabilidad en cualquier modelo de regresión. Para una regresión lineal simple, la precisión de cada valor se mide por su residual al cuadrado, donde un residual es la diferencia entre el valor observado (de los datos) y el valor predicho (basado en un modelo de los datos, por ejemplo, una línea de regresión ). Dada una línea de mejor ajuste, el residual es la diferencia vertical entre los datos y la línea de mejor ajuste. Esto se muestra en la siguiente figura.
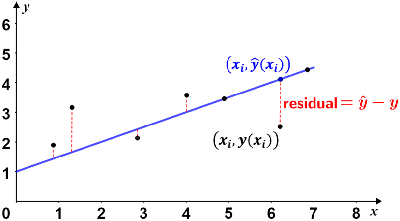
Si el punto de datos se encuentra por encima de la línea de mejor ajuste, el residual es positivo; si está por debajo de la línea, el residual es negativo; los puntos de datos que se encuentran en la línea de regresión tienen residuos de 0. En la figura se muestran dos de esos puntos.
Regresión lineal múltiple
La regresión lineal múltiple se diferencia de la regresión lineal simple en que considera múltiples variables independientes. Por ejemplo, el ejemplo de regresión lineal simple anterior solo usó una sola variable independiente (el tamaño del tanque de gasolina) y estudió su relación con la distancia que el automóvil podría viajar. Hay otros factores que pueden determinar qué tan lejos puede viajar un automóvil, además del tanque de gasolina solo. Para considerar otros factores, como el tamaño del motor, si el automóvil es un híbrido, si tiene tracción en las cuatro ruedas y más, se puede usar la regresión lineal múltiple.
La regresión lineal múltiple se puede modelar utilizando la siguiente ecuación
es la variable dependiente, β 0 es el valor inicial de la variable dependiente y β i es el cambio en la variable dependiente por cada cambio de unidad en la i ésima variable independiente.



