Ley de los senos

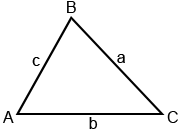
En trigonometría, la Ley de los senos relaciona los s ides y ángulos de triángulos . Dado el triángulo de abajo, donde A, B y C son las medidas de los ángulos del triángulo, y a, byc son sus lados, la Ley de los senos establece:

Generalmente, el formato de la izquierda se usa para encontrar un lado desconocido, mientras que el formato de la derecha se usa para encontrar un ángulo desconocido.

La definición de triángulo rectángulo de sine () solo se puede utilizar con triángulos rectángulos. No se puede usar para relacionar los lados y ángulos de triángulos oblicuos (no rectos). Sin embargo, hay muchas otras relaciones que podemos usar cuando trabajamos con triángulos oblicuos. La Ley de los senos es una de esas relaciones. Otra es la Ley de los cosenos .

Cuándo usar la ley de los senos

La ley de los senos se puede utilizar para resolver los lados y ángulos de un triángulo oblicuo cuando se conocen las siguientes medidas:

• Dos ángulos y un lado: AAS (ángulo-ángulo-lado) o ASA (ángulo-lado-ángulo)
• Dos lados y un ángulo no incluido: SSA (ángulo lateral)

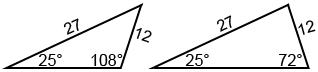
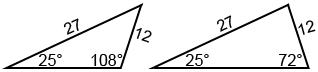
Prueba de la ley de los senos

Para mostrar cómo funciona la Ley de los senos, dibuje la altitud h desde el ángulo B hacia el lado b, como se muestra a continuación.

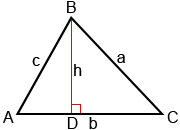
La altitud h divide el triángulo ABC en triángulos rectángulos ADB y CDB. Luego podemos usar la definición de triángulo rectángulo de seno,

Triángulo ADB:

Triángulo CDB:

Establecer estos dos valores de h iguales entre sí:

a · sin (C)=c · sin (A)

A continuación, dibuje la altitud h desde el ángulo A en lugar de B, como se muestra a continuación.

Para los triángulos recién formados ADB y CDB,

Triángulo ADB:

Triángulo CDB:

Establecer estos dos valores de h iguales entre sí:

b · sin (C)=c · sin (B)

Usando la propiedad transitiva, podemos unir estos dos conjuntos de ecuaciones para obtener la Ley de los senos:

scaleim

y

scaleimg