Los vectores son objetos matemáticos que codifican magnitud y dirección. Los vectores son omnipresentes en física y describen cantidades como fuerza, velocidad, campo eléctrico, etc.
Hay 2 formas comunes de pensar en los vectores: geométrica y numéricamente. En la mentalidad geométrica, los vectores se consideran flechas que apuntan en una dirección determinada con una longitud o magnitud determinada:
Para describir un vector v numéricamente, primero elegimos un sistema de coordenadas cuyo origen está al comienzo de la flecha. Luego asociamos el vector con las coordenadas de la punta de flecha:
También podemos tener vectores en tres dimensiones o más:
Escribiríamos v como:
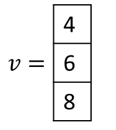
o como v=[4, 6, 8 ] T . El exponente T significa «transponer» y significa tomar el vector de fila, [4, 6, 8 ] y voltear o transponerlo a un vector de columna de modo que la entrada más a la izquierda se convierta en la parte superior y la más a la derecha en la parte inferior. La dimensión de un vector es el número de coordenadas que tiene. En el ejemplo anterior, dado que v tiene 3 coordenadas, 4, 6, y 8 , decimos que v es tridimensional. A continuación, v , es de 4 dimensiones, w es de 5 dimensiones y x es de 6 dimensiones:
Adición de vectores
Si elegimos un sistema de coordenadas, escribimos v y w como vectores de columna y simplemente sumamos las coordenadas respectivas para obtener v + w .
Observe que el orden de la suma no importa, por lo que v + w=w + v . Geométricamente, esto se representa comenzando desde el origen O , desplazándose por el vector v para llegar a S , luego desplazando por vector w para llegar a P . Entonces v + w es el vector de O a P . También podríamos cambiar primero en w para llegar a T , luego cambiar en v pero aún llegaríamos al mismo punto final P , entonces v + w=w + v en la definición geométrica como bueno.
Nota: Solo se pueden agregar vectores de la misma dimensión. Por ejemplo, no podemos agregar v =[1, 2, 3 ] T y w =[4, 5 ] T porque v es tridimensional y w es bidimensional. Pero podemos agregar v=[3, -1, 4 ] T y w=[5, 9, -6 ] T para obtener v + w=[3 + 5, -1 + 9, 4 – 6 ] T =[8, 8, -2 ] T .
Multiplicación de vectores por escalares
Dado un sistema de coordenadas, podemos multiplicar un vector v con un número c , llamado escalar, multiplicando cada coordenada de v por c :
Geométricamente, el vector cv se encuentra en la misma línea que v excepto que está escalado por un factor de c , por lo que c se llama escalar. Si | c | & gt; 1 , cv será más grande o tendrá una magnitud mayor que v . Si c & gt; 0 , cv apuntará en la misma dirección que v . Si c & lt; 0 , cv apuntará en la dirección opuesta a v . El diagrama muestra que v se multiplica por – 1 y 2 :
Resta de vectores
Para restar 2 vectores v y w para obtener v – w , calculamos las coordenadas de v menos las coordenadas correspondientes de w .
v – w debe ser un vector que satisfaga w + (v – w)=v . Por lo tanto, utilizando nuestro conocimiento de la suma de vectores, el siguiente diagrama da una interpretación geométrica de v – w como el vector del encabezado de w al encabezado de v .
Tenga en cuenta que v – w=v + (-1) * w , que es v más w escalado por un factor de – 1 . Al igual que con la suma de vectores, solo podemos restar vectores de la misma dimensión.
Consulte también magnitud .



